Question Number 16638 by tawa tawa last updated on 24/Jun/17
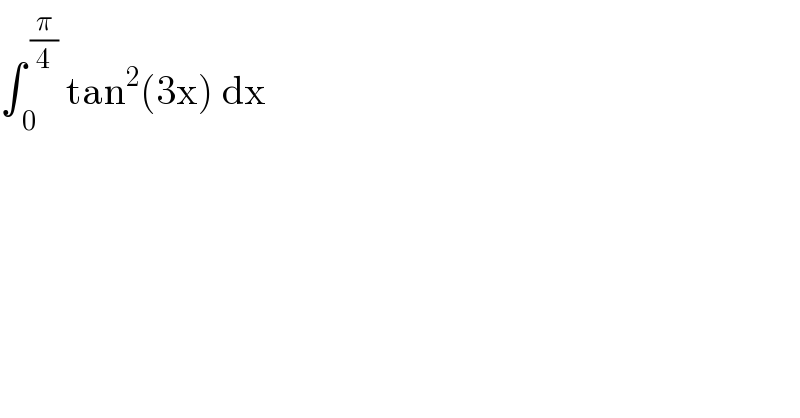
$$\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\mathrm{tan}^{\mathrm{2}} \left(\mathrm{3x}\right)\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 24/Jun/17
![∫_0 ^( π/4) [sec^2 (3x)−1]dx = (((tan 3x)/3)−x)∣_0 ^(π/4) =−(1/3)−(π/4) .](https://www.tinkutara.com/question/Q16640.png)
$$\:\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left[\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{3x}\right)−\mathrm{1}\right]\mathrm{dx} \\ $$$$\:\:\:\:\:\:=\:\left(\frac{\mathrm{tan}\:\mathrm{3x}}{\mathrm{3}}−\mathrm{x}\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\pi}{\mathrm{4}}\:. \\ $$
Commented by tawa tawa last updated on 24/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
