Menu Close

0-pi-4-tan-x-1-tan-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 129105 by I want to learn more last updated on 12/Jan/21
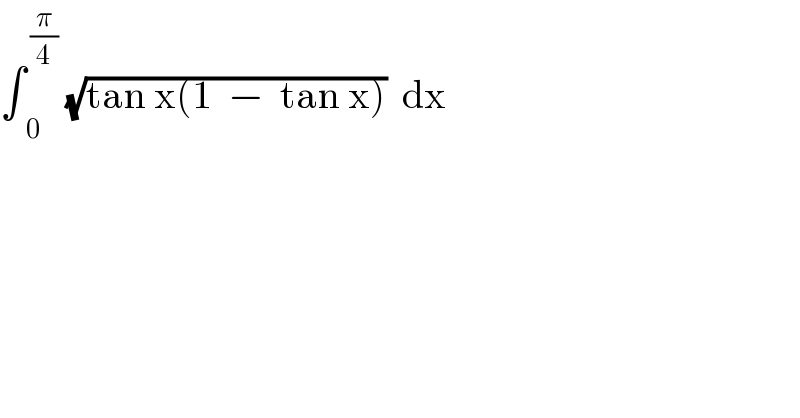
∫_( 0) ^( (π/4)) (√(tan x(1 − tan x))) dx
$$\int_{\:\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\sqrt{\mathrm{tan}\:\mathrm{x}\left(\mathrm{1}\:\:−\:\:\mathrm{tan}\:\mathrm{x}\right)}\:\:\mathrm{dx} \\ $$
Answered by Lordose last updated on 13/Jan/21
Ω = ∫_0 ^(π/4) (√(tan(x)))(√(1−tan(x)))dx =^(u=tan(x)) ∫_0 ^( 1) ((u^(1/2) (√(1−u)))/(1+u^2 ))du Ω = ∫_0 ^( 1) u^(1/2) (1−u)^(1/2) Σ_(n=0) ^∞ (−1)^n u^(2n) du = Σ_(n=0) ^∞ (−1)^n ∫_0 ^( 1) u^(2n+(1/2)) (1−u)^(1/2) du 𝛃(x,y) = ∫_0 ^( 1) t^(x−1) (1−t)^(y−1) dt Ω = Σ_(n=0) ^∞ (−1)^n (𝛃(((4n+3)/2),(3/2))) = Σ_(n=0) ^∞ (−1)^n (((𝚪(((4n+3)/2))𝚪((3/2)))/(𝚪(2n+3)))) Ω = ((√π)/2)Σ_(n=0) ^∞ (−1)^n (((𝚪(((4n+3)/2)))/(𝚪(2n+3)))) = ((√π)/2)((√π)((√(2(1+(√2))))−2) = (π/2)((√(2(1+(√2))))−2) ★L𝛗rD ∅sE
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{tan}\left(\mathrm{x}\right)}\sqrt{\mathrm{1}−\mathrm{tan}\left(\mathrm{x}\right)}\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{tan}\left(\mathrm{x}\right)} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}−\mathrm{u}}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:\: \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}^{\mathrm{2n}} \mathrm{du}\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{du}\:\: \\ $$$$\boldsymbol{\beta}\left(\mathrm{x},\mathrm{y}\right)\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{t}^{\mathrm{x}−\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{y}−\mathrm{1}} \mathrm{dt} \\ $$$$\Omega\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\boldsymbol{\beta}\left(\frac{\mathrm{4n}+\mathrm{3}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\right)\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{4n}+\mathrm{3}}{\mathrm{2}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{2n}+\mathrm{3}\right)}\right) \\ $$$$\Omega\:=\:\frac{\sqrt{\pi}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{4n}+\mathrm{3}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{2n}+\mathrm{3}\right)}\right)\:=\:\frac{\sqrt{\pi}}{\mathrm{2}}\left(\sqrt{\pi}\left(\sqrt{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}−\mathrm{2}\right)\:=\:\frac{\pi}{\mathrm{2}}\left(\sqrt{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}−\mathrm{2}\right)\right. \\ $$$$\bigstar\boldsymbol{\mathrm{L}\phi\mathrm{rD}}\:\boldsymbol{\varnothing\mathrm{sE}} \\ $$
Commented by MJS_new last updated on 13/Jan/21
great!
$$\mathrm{great}! \\ $$
Commented by I want to learn more last updated on 13/Jan/21
Thanks sir.
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Answered by MJS_new last updated on 13/Jan/21
∫(√((1−tan x)tan x)) dx= [t=(√((1/(tan x))−1)) → dx=−((2(√((1−tan x)tan^3 x)))/(1+tan^2 x))dt] =−2∫(t^2 /((t^2 +1)(t^4 +2t^2 +2)))dt= =−2∫(t^2 /((t^2 +1)(t^2 −(√(−2+2(√2))) t+(√2))(t^2 +(√(−2+2(√2))) t+(√2))))dt= =−2∫(t^2 /((t^2 +1)(t^2 −at+b)(t^2 +at+b)))dt= =2∫(dt/(t^2 +1))+((√(−2+2(√2)))/2)(∫((t−2(√(1+(√2))))/(t^2 −(√(−2+2(√2))) t+(√2)))dt−∫((t+2(√(1+(√2))))/(t^2 +(√(−2+2(√2))) t+(√2)))dt) and these can be solved using the usual formulas in the end I get (((√(2+2(√2)))/2)−1)π
$$\int\sqrt{\left(\mathrm{1}−\mathrm{tan}\:{x}\right)\mathrm{tan}\:{x}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{\mathrm{1}}{\mathrm{tan}\:{x}}−\mathrm{1}}\:\rightarrow\:{dx}=−\frac{\mathrm{2}\sqrt{\left(\mathrm{1}−\mathrm{tan}\:{x}\right)\mathrm{tan}^{\mathrm{3}} \:{x}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}}{dt}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}\right)}{dt}= \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}\:{t}+\sqrt{\mathrm{2}}\right)\left({t}^{\mathrm{2}} +\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}\:{t}+\sqrt{\mathrm{2}}\right)}{dt}= \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −{at}+{b}\right)\left({t}^{\mathrm{2}} +{at}+{b}\right)}{dt}= \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{2}}\left(\int\frac{{t}−\mathrm{2}\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}}}{{t}^{\mathrm{2}} −\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}\:{t}+\sqrt{\mathrm{2}}}{dt}−\int\frac{{t}+\mathrm{2}\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}}}{{t}^{\mathrm{2}} +\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}\:{t}+\sqrt{\mathrm{2}}}{dt}\right) \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{formulas} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{end}\:\mathrm{I}\:\mathrm{get} \\ $$$$\left(\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{2}}−\mathrm{1}\right)\pi \\ $$
Commented by I want to learn more last updated on 13/Jan/21
Thanks sir.
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *