Menu Close

0-pi-4-x-2-x-sin-x-cos-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 118111 by bemath last updated on 15/Oct/20
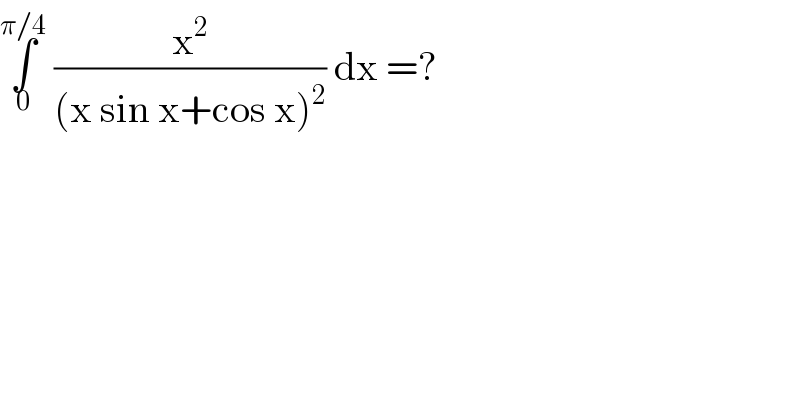
∫_0 ^(π/4) (x^2 /((x sin x+cos x)^2 )) dx =?
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{dx}\:=? \\ $$
Answered by Lordose last updated on 15/Oct/20
Ω=∫_0 ^( (π/4)) (x^2 /((xsinx+cosx)^2 ))dx Ω=∫_( 0) ^( (π/4)) ((x^2 sin^2 x+x^2 cos^2 x)/((xsinx+cosx)^2 ))dx Ω=∫_( 0) ^( (π/4)) ((x^2 sin^2 x+xsinxcosx)/((xsinx+cosx)^2 ))dx + ∫_( 0) ^( (π/4)) ((x^2 cos^2 x−xsinxcosx)/((xsinx+cosx)^2 ))dx Ω=∫_( 0) ^( (π/4)) ((xsinx(xsinx+cosx))/((xsinx+cosx)^2 ))dx + ∫_( 0) ^( (π/4)) ((−xcosx(−xcosx+sinx))/((xsinx+cosx)^2 ))dx Ω=Φ + Λ resolving Λ by IBP u=sinx−xcosx ⇒ du= xsinxdx dv=((−xcosx)/((xsinx+cosx)^2 ))dx ⇒ v=(1/(xsinx+cosx)) Λ=∣((sinx−xcosx)/(xsinx+cosx))∣_0 ^(π/4) − ∫_( 0) ^( (π/4)) (( xsinx)/(xsinx+cosx))dx Λ=∣((sinx−xcosx)/(xsinx+cosx))∣_0 ^(π/4) − Φ Ω= Φ+∣((sinx−xcosx)/(xsinx+cosx))∣_0 ^(π/4) −Φ Ω=∣((sinx−xcosx)/(xsinx+cosx))∣_0 ^(π/4) Ω=((4−π)/(4+π))
$$ \\ $$$$\Omega=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega=\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{x}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega=\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{xsinxcosx}}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}\:+\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{xsinxcosx}}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega=\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{xsinx}\left(\mathrm{xsinx}+\mathrm{cosx}\right)}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}\:+\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{−\mathrm{xcosx}\left(−\mathrm{xcosx}+\mathrm{sinx}\right)}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega=\Phi\:+\:\Lambda \\ $$$$\mathrm{resolving}\:\Lambda\:\mathrm{by}\:\mathrm{IBP} \\ $$$$\mathrm{u}=\mathrm{sinx}−\mathrm{xcosx}\:\Rightarrow\:\mathrm{du}=\:\mathrm{xsinxdx} \\ $$$$\mathrm{dv}=\frac{−\mathrm{xcosx}}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\:\mathrm{v}=\frac{\mathrm{1}}{\mathrm{xsinx}+\mathrm{cosx}} \\ $$$$\Lambda=\mid\frac{\mathrm{sinx}−\mathrm{xcosx}}{\mathrm{xsinx}+\mathrm{cosx}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\:\mathrm{xsinx}}{\mathrm{xsinx}+\mathrm{cosx}}\mathrm{dx} \\ $$$$\Lambda=\mid\frac{\mathrm{sinx}−\mathrm{xcosx}}{\mathrm{xsinx}+\mathrm{cosx}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−\:\Phi \\ $$$$\Omega=\:\Phi+\mid\frac{\mathrm{sinx}−\mathrm{xcosx}}{\mathrm{xsinx}+\mathrm{cosx}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −\Phi \\ $$$$\Omega=\mid\frac{\mathrm{sinx}−\mathrm{xcosx}}{\mathrm{xsinx}+\mathrm{cosx}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$\Omega=\frac{\mathrm{4}−\pi}{\mathrm{4}+\pi} \\ $$$$ \\ $$
Commented by bemath last updated on 15/Oct/20
gave kudos
$${gave}\:{kudos} \\ $$
Answered by Ar Brandon last updated on 15/Oct/20
(d/dx)(xsinx+cosx)=xcosx+sinx−sinx=xcosx I=∫_0 ^(π/4) (x^2 /((xsinx+cosx)^2 ))dx=∫_0 ^(π/4) ((xcosx)/((xsinx+cosx)^2 ))∙(x/(cosx))dx ={(x/(cosx))∫((xcosx)/((xsinx+cosx)^2 ))dx}_0 ^(π/4) −∫_0 ^(π/4) {(d/dx)((x/(cosx)))∙∫((xcosx)/((xsinx+cosx)^2 ))dx} =−[(x/(cosx))∙(1/(xsinx+cosx))]_0 ^(π/4) +∫_0 ^(π/4) {(((cosx+xsinx)/(cos^2 x)))((1/(xsinx+cosx)))}dx =−[(x/(cosx))∙(1/(xsinx+cosx))]_0 ^(π/4) +∫_0 ^(π/4) (dx/(cos^2 x)) =[tanx−(x/(cosx))∙(1/(xsinx+cosx))]_0 ^(π/4) =[1−((2π)/(4(√2)))∙(8/(π(√2)+4(√2)))] =1−((16π)/(8π+32))=((8π+32−16π)/(8π+32))=((32−8π)/(32+8π))=((4−π)/(4+π))
$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{xsinx}+\mathrm{cosx}\right)=\mathrm{xcosx}+\mathrm{sinx}−\mathrm{sinx}=\mathrm{xcosx} \\ $$$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{xcosx}}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\centerdot\frac{\mathrm{x}}{\mathrm{cosx}}\mathrm{dx} \\ $$$$\:\:\:=\left\{\frac{\mathrm{x}}{\mathrm{cosx}}\int\frac{\mathrm{xcosx}}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}\right\}_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{x}}{\mathrm{cosx}}\right)\centerdot\int\frac{\mathrm{xcosx}}{\left(\mathrm{xsinx}+\mathrm{cosx}\right)^{\mathrm{2}} }\mathrm{dx}\right\} \\ $$$$\:\:\:=−\left[\frac{\mathrm{x}}{\mathrm{cosx}}\centerdot\frac{\mathrm{1}}{\mathrm{xsinx}+\mathrm{cosx}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left\{\left(\frac{\mathrm{cosx}+\mathrm{xsinx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\right)\left(\frac{\mathrm{1}}{\mathrm{xsinx}+\mathrm{cosx}}\right)\right\}\mathrm{dx} \\ $$$$\:\:\:=−\left[\frac{\mathrm{x}}{\mathrm{cosx}}\centerdot\frac{\mathrm{1}}{\mathrm{xsinx}+\mathrm{cosx}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:=\left[\mathrm{tanx}−\frac{\mathrm{x}}{\mathrm{cosx}}\centerdot\frac{\mathrm{1}}{\mathrm{xsinx}+\mathrm{cosx}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\left[\mathrm{1}−\frac{\mathrm{2}\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\centerdot\frac{\mathrm{8}}{\pi\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{2}}}\right] \\ $$$$\:\:\:=\mathrm{1}−\frac{\mathrm{16}\pi}{\mathrm{8}\pi+\mathrm{32}}=\frac{\mathrm{8}\pi+\mathrm{32}−\mathrm{16}\pi}{\mathrm{8}\pi+\mathrm{32}}=\frac{\mathrm{32}−\mathrm{8}\pi}{\mathrm{32}+\mathrm{8}\pi}=\frac{\mathrm{4}−\pi}{\mathrm{4}+\pi} \\ $$
Commented by bemath last updated on 15/Oct/20
santuyy
$${santuyy} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *