Question Number 159854 by mnjuly1970 last updated on 21/Nov/21
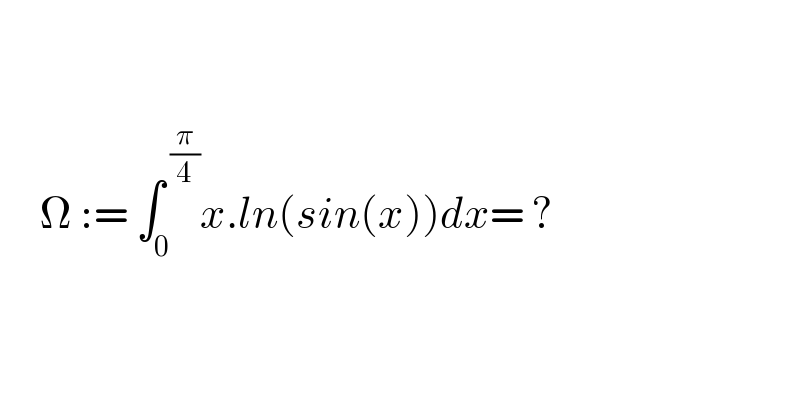
$$ \\ $$$$ \\ $$$$\:\:\:\:\:\Omega\::=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {x}.{ln}\left({sin}\left({x}\right)\right){dx}=\:? \\ $$$$ \\ $$$$ \\ $$
Answered by mindispower last updated on 22/Nov/21
![ln(sin(x))=−ln(2)−Σ_(n≥1) ((cos(2nx))/n) Ω=∫_0 ^(π/4) x(−ln(2)−Σ((cos(2nx))/n))dx =−((ln(2))/(32))π^2 −Σ_(n≥1) (1/n)∫_0 ^(π/4) cos(2nx)xdx =−((ln(2))/(32))π^2 −Σ_(n≥1) (1/n)[((sin(n(π/2)))/(2n)).(π/4)−(1/(2n))∫_0 ^(π/4) sin(2nx)dx =−((ln(2)π^2 )/(32))+Σ_(n≥1) (−(π/8).((sin(((nπ)/2)))/n^2 )−(1/(4n^3 ))[cos(((nπ)/2))−1]) =−((ln(2)π^2 )/(32))−(π/8).Σ_(n≥0) (((−1)^n )/((2n+1)^2 ))−(1/4)Σ_(n≥1) (((−1)^n )/(8n^3 ))+((ζ(3))/4) =((−ln(2))/(32))π^2 −(π/8)G+((ζ(3))/4)−(1/(32))((1/4)−1)ζ(3) =−((ln(2))/(32))π^2 −(π/8)G+((35)/(128))ζ(3)](https://www.tinkutara.com/question/Q159932.png)
$${ln}\left({sin}\left({x}\right)\right)=−{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}\left(−{ln}\left(\mathrm{2}\right)−\Sigma\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}}\right){dx} \\ $$$$=−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{32}}\pi^{\mathrm{2}} −\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cos}\left(\mathrm{2}{nx}\right){xdx} \\ $$$$=−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{32}}\pi^{\mathrm{2}} −\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\left[\frac{{sin}\left({n}\frac{\pi}{\mathrm{2}}\right)}{\mathrm{2}{n}}.\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {sin}\left(\mathrm{2}{nx}\right){dx}\right. \\ $$$$=−\frac{{ln}\left(\mathrm{2}\right)\pi^{\mathrm{2}} }{\mathrm{32}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\frac{\pi}{\mathrm{8}}.\frac{{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{3}} }\left[{cos}\left(\frac{{n}\pi}{\mathrm{2}}\right)−\mathrm{1}\right]\right) \\ $$$$=−\frac{{ln}\left(\mathrm{2}\right)\pi^{\mathrm{2}} }{\mathrm{32}}−\frac{\pi}{\mathrm{8}}.\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{8}{n}^{\mathrm{3}} }+\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{4}} \\ $$$$=\frac{−{ln}\left(\mathrm{2}\right)}{\mathrm{32}}\pi^{\mathrm{2}} −\frac{\pi}{\mathrm{8}}{G}+\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{32}}\left(\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}\right)\zeta\left(\mathrm{3}\right) \\ $$$$=−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{32}}\pi^{\mathrm{2}} −\frac{\pi}{\mathrm{8}}{G}+\frac{\mathrm{35}}{\mathrm{128}}\zeta\left(\mathrm{3}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 23/Nov/21

$${thanks}\:{alot}\:\:{sir}\:\mathrm{Power}… \\ $$
Commented by mindispower last updated on 23/Nov/21
$${withe}\:{pleasur}\:{sir}\:{have}\:{a}\:{nice}\:{day} \\ $$
