Question Number 159680 by cortano last updated on 20/Nov/21
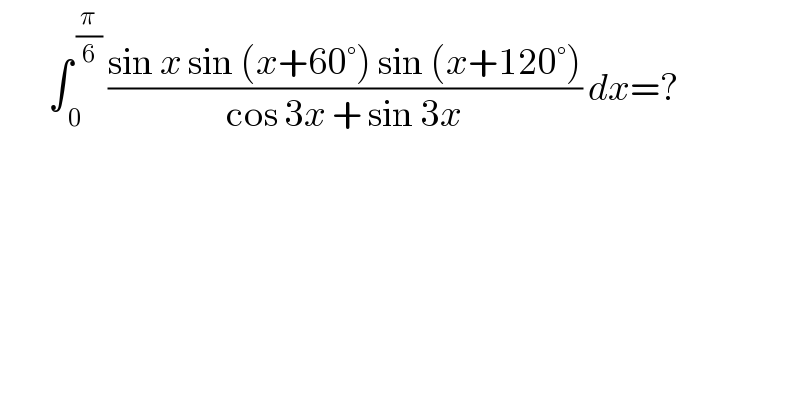
$$\:\:\:\:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{6}}} \:\frac{\mathrm{sin}\:{x}\:\mathrm{sin}\:\left({x}+\mathrm{60}°\right)\:\mathrm{sin}\:\left({x}+\mathrm{120}°\right)}{\mathrm{cos}\:\mathrm{3}{x}\:+\:\mathrm{sin}\:\mathrm{3}{x}}\:{dx}=? \\ $$
Commented by cortano last updated on 20/Nov/21
![let θ=3x ⇒I=(1/(12))∫_0 ^( (π/2)) ((sin θ)/(cos θ+sin θ)) dθ 2I= (1/(12))∫_( 0) ^( (π/2)) ((sin θ+cos θ)/(cos θ+sin θ)) dθ I= (1/(24)) ∫_( 0) ^( (π/2)) dθ = [(θ/(24)) ]_0 ^(π/2) = (π/(48))](https://www.tinkutara.com/question/Q159688.png)
$$\:{let}\:\theta=\mathrm{3}{x}\:\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{12}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}\:\:\theta}{\mathrm{cos}\:\theta+\mathrm{sin}\:\theta}\:{d}\theta \\ $$$$\mathrm{2}{I}=\:\frac{\mathrm{1}}{\mathrm{12}}\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}\:\theta+\mathrm{cos}\:\theta}{\mathrm{cos}\:\theta+\mathrm{sin}\:\theta}\:{d}\theta \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{24}}\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:{d}\theta\:=\:\left[\frac{\theta}{\mathrm{24}}\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\:\frac{\pi}{\mathrm{48}}\: \\ $$
Commented by tounghoungko last updated on 20/Nov/21

$$\:\Rightarrow\mathrm{sin}\:\left({x}+\mathrm{60}°\right)\mathrm{sin}\:\left({x}+\mathrm{120}°\right)\: \\ $$$$=\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}\:{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}\right) \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} {x}\:=\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\Rightarrow\:\mathrm{sin}\:{x}\left(\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{3}{x}\: \\ $$$$\:\:{I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{6}}} \:\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{cos}\:\mathrm{3}{x}+\mathrm{sin}\:\mathrm{3}{x}}\:{dx} \\ $$$$\: \\ $$
