Question Number 96979 by M±th+et+s last updated on 05/Jun/20
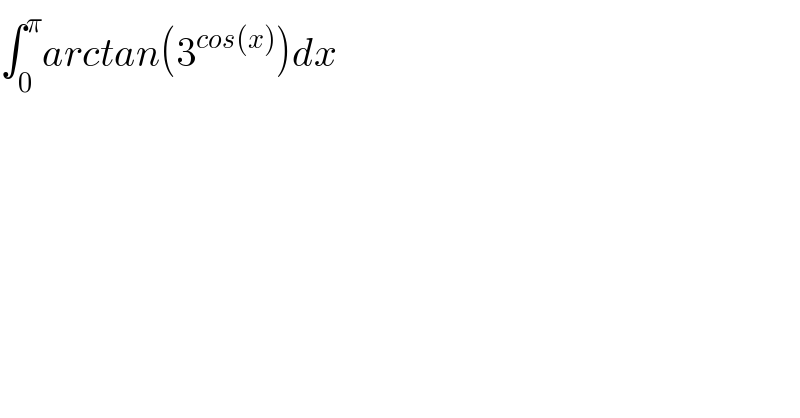
$$\int_{\mathrm{0}} ^{\pi} {arctan}\left(\mathrm{3}^{{cos}\left({x}\right)} \right){dx} \\ $$
Answered by MJS last updated on 06/Jun/20
![y=arctan 3^(cos x) ; x∈[0; π] this is point symmetric, the center is C= (((π/2)),((π/4)) ) ⇒ the value of the integral is (π^2 /4)](https://www.tinkutara.com/question/Q96984.png)
$${y}=\mathrm{arctan}\:\mathrm{3}^{\mathrm{cos}\:{x}} ;\:{x}\in\left[\mathrm{0};\:\pi\right] \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{point}\:\mathrm{symmetric},\:\mathrm{the}\:\mathrm{center}\:\mathrm{is} \\ $$$${C}=\begin{pmatrix}{\frac{\pi}{\mathrm{2}}}\\{\frac{\pi}{\mathrm{4}}}\end{pmatrix} \\ $$$$\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{is}\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Commented by M±th+et+s last updated on 06/Jun/20

$${well}\:{done}\:{sir}\: \\ $$
Commented by M±th+et+s last updated on 06/Jun/20

$${sir}\:{mjs}\:{can}\:{you}\:{explain}\:{the}\:{rule}\:{and} \\ $$$${when}\:{can}\:{i}\:{use}\:{it}\:{and}\:{thank}\:{you} \\ $$
Commented by MJS last updated on 06/Jun/20

$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{find}\:\mathrm{out}\:\mathrm{if}\:\mathrm{there}'\mathrm{s}\:\mathrm{some}\:\mathrm{kind}\:\mathrm{of} \\ $$$$\mathrm{symmetry}\:\mathrm{within}\:\mathrm{the}\:\mathrm{interval}…\:\mathrm{I}'\mathrm{m}\:\mathrm{not} \\ $$$$\mathrm{sure}\:\mathrm{if}\:\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{rule} \\ $$$$\mathrm{here} \\ $$$$\mathrm{arctan}\:\frac{\mathrm{1}}{\alpha}\:=−\mathrm{arctan}\:\alpha \\ $$$$\alpha=\mathrm{3}^{\mathrm{cos}\:{x}} ;\:−\mathrm{1}\leqslant\mathrm{cos}\:{x}\:\leqslant\mathrm{1}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{3}}\leqslant\alpha\leqslant\mathrm{3} \\ $$$$\Rightarrow\:\mathrm{center}\:\mathrm{is}\:\mathrm{at}\:\mathrm{cos}\:{x}\:=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Commented by M±th+et+s last updated on 06/Jun/20

$${thanx} \\ $$
