Question Number 118891 by cantor last updated on 20/Oct/20
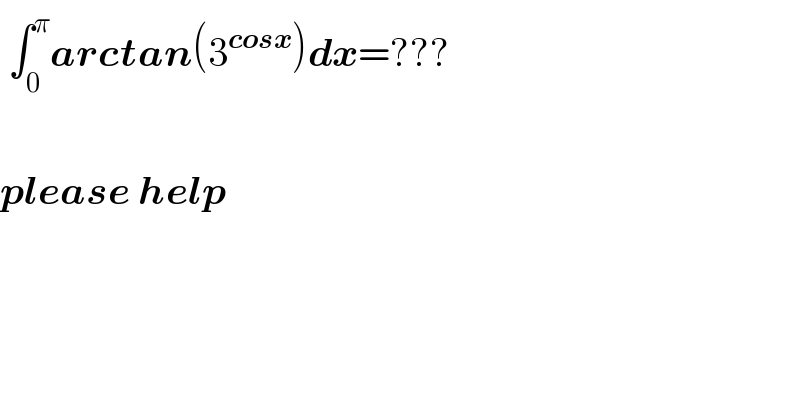
$$\:\int_{\mathrm{0}} ^{\pi} \boldsymbol{{arctan}}\left(\mathrm{3}^{\boldsymbol{{cosx}}} \right)\boldsymbol{{dx}}=??? \\ $$$$ \\ $$$$\boldsymbol{{please}}\:\boldsymbol{{help}} \\ $$
Answered by Dwaipayan Shikari last updated on 20/Oct/20
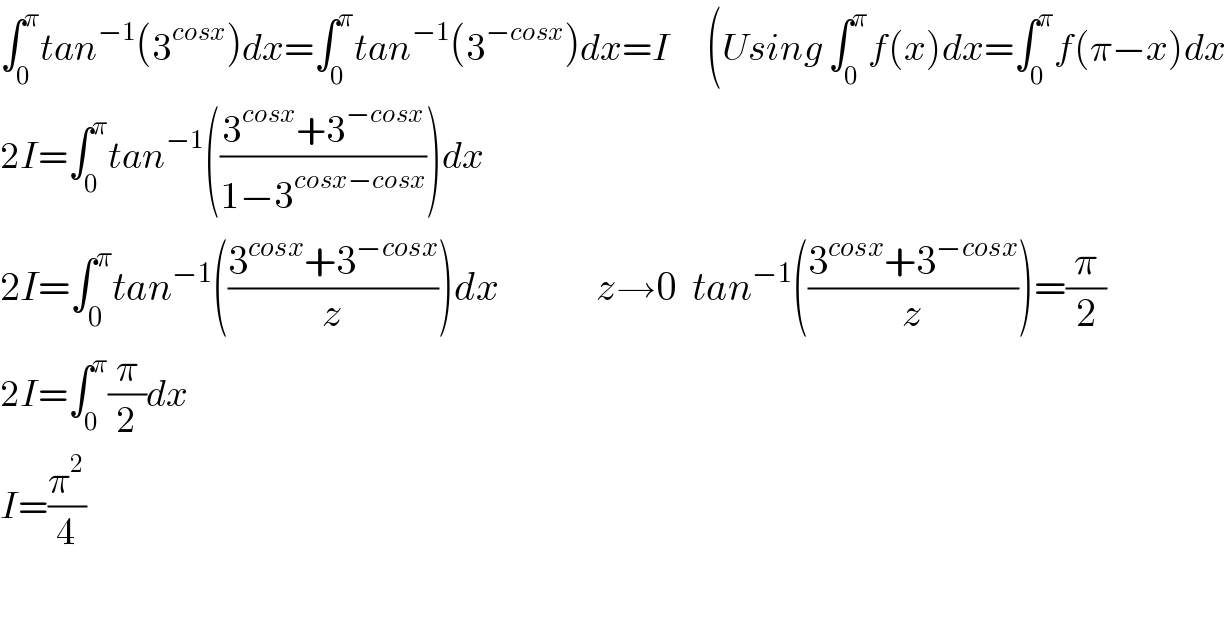
$$\int_{\mathrm{0}} ^{\pi} {tan}^{−\mathrm{1}} \left(\mathrm{3}^{{cosx}} \right){dx}=\int_{\mathrm{0}} ^{\pi} {tan}^{−\mathrm{1}} \left(\mathrm{3}^{−{cosx}} \right){dx}={I}\:\:\:\:\:\:\left({Using}\:\int_{\mathrm{0}} ^{\pi} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\pi} {f}\left(\pi−{x}\right){dx}\right. \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} {tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}^{{cosx}} +\mathrm{3}^{−{cosx}} }{\mathrm{1}−\mathrm{3}^{{cosx}−{cosx}} }\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} {tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}^{{cosx}} +\mathrm{3}^{−{cosx}} }{{z}}\right){dx}\:\:\:\:\:\:\:\:\:\:\:\:{z}\rightarrow\mathrm{0}\:\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}^{{cosx}} +\mathrm{3}^{−{cosx}} }{{z}}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{2}}{dx}\:\:\:\:\:\:\:\:\: \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 20/Oct/20
![let me explain. note:: tan^(−1) (x)+tan^(−1) (y)=tan^(−1) (((x+y)/(1−xy))) I=∫_(0 ) ^( π) tan^(−1) (3^(cos(x)) )dx.....(1) I =^([∫_a ^( b) f(x)dx=∫_a ^( b) f(a+b−x)dx]) ∫_0 ^( π) tan^(−1) (3^(−cos(x)) )...(2) ∴(1)+(2):: 2I=^(note) ∫_0 ^( π) tan^(−1) (((3^(cos(x)) +3^(−cos(x)) )/([1−3^(cos(x)) .3^(−cos(x)) ]=0))) =∫_0 ^( π) [tan^(−1) (∞)=(π/2)]dx=(π^2 /2) ∴ I=(π^2 /4) ✓✓ ... m.n.1970...](https://www.tinkutara.com/question/Q118904.png)
$${let}\:{me}\:{explain}. \\ $$$${note}::\:{tan}^{−\mathrm{1}} \left({x}\right)+{tan}^{−\mathrm{1}} \left({y}\right)={tan}^{−\mathrm{1}} \left(\frac{{x}+{y}}{\mathrm{1}−{xy}}\right) \\ $$$${I}=\int_{\mathrm{0}\:} ^{\:\pi} {tan}^{−\mathrm{1}} \left(\mathrm{3}^{{cos}\left({x}\right)} \right){dx}…..\left(\mathrm{1}\right) \\ $$$${I}\:\:\:\overset{\left[\int_{{a}} ^{\:{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{\:{b}} {f}\left({a}+{b}−{x}\right){dx}\right]} {=}\int_{\mathrm{0}} ^{\:\pi} {tan}^{−\mathrm{1}} \left(\mathrm{3}^{−{cos}\left({x}\right)} \right)…\left(\mathrm{2}\right) \\ $$$$\therefore\left(\mathrm{1}\right)+\left(\mathrm{2}\right)::\: \\ $$$$\mathrm{2}{I}\overset{{note}} {=}\int_{\mathrm{0}} ^{\:\:\pi} {tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}^{{cos}\left({x}\right)} +\mathrm{3}^{−{cos}\left({x}\right)} }{\left[\mathrm{1}−\mathrm{3}^{{cos}\left({x}\right)} .\mathrm{3}^{−{cos}\left({x}\right)} \right]=\mathrm{0}}\right) \\ $$$$\:\:\:\:\:\:\: \\ $$$$=\int_{\mathrm{0}} ^{\:\pi} \left[{tan}^{−\mathrm{1}} \left(\infty\right)=\frac{\pi}{\mathrm{2}}\right]{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\therefore\:\:{I}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\:\:\:\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:…\:{m}.{n}.\mathrm{1970}… \\ $$
Commented by cantor last updated on 20/Oct/20

$$\boldsymbol{{please}}\:\boldsymbol{{i}}\:\boldsymbol{{don}}'\boldsymbol{{t}}\:\boldsymbol{{understand}} \\ $$$$\boldsymbol{{the}}\:\mathrm{1}^{\boldsymbol{{st}}} \:\boldsymbol{{line}}\:\boldsymbol{{please}}\:\boldsymbol{{explaint}} \\ $$
Commented by benjo_mathlover last updated on 20/Oct/20

$${replace}\:{x}\:{by}\:\pi−{x}\: \\ $$
Answered by mindispower last updated on 20/Oct/20
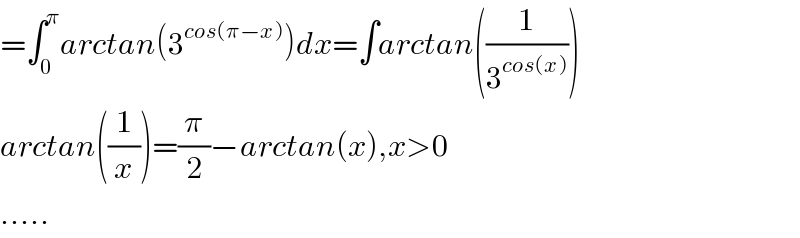
$$=\int_{\mathrm{0}} ^{\pi} {arctan}\left(\mathrm{3}^{{cos}\left(\pi−{x}\right)} \right){dx}=\int{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}^{{cos}\left({x}\right)} }\right) \\ $$$${arctan}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\pi}{\mathrm{2}}−{arctan}\left({x}\right),{x}>\mathrm{0} \\ $$$$….. \\ $$
