Question Number 149113 by bramlexs22 last updated on 03/Aug/21
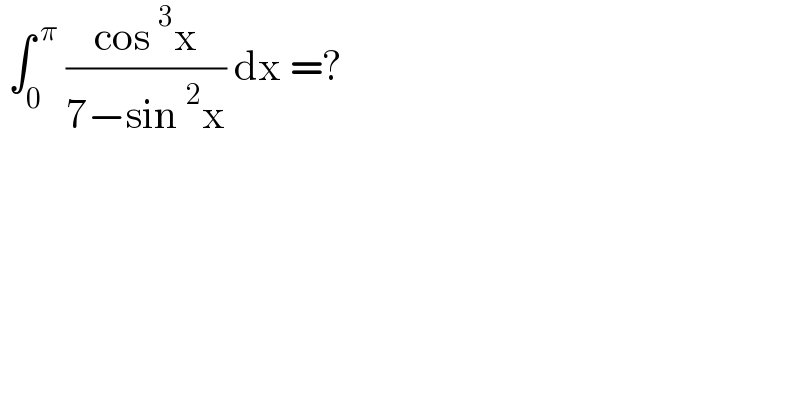
$$\:\int_{\mathrm{0}} ^{\:\pi} \:\frac{\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{7}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:=? \\ $$
Answered by mathmax by abdo last updated on 03/Aug/21
![Ψ=∫_0 ^(π ) ((cos^3 x)/(7−sin^2 x)) dx ⇒Ψ=∫_0 ^π ((cos^3 x)/(7−(1−cos^2 x)))dx =∫_0 ^π ((cos^3 x)/(6+cos^2 x))dx =∫_0 ^π ((cosx(cos^2 x+6)−6cosx)/(cos^2 x +6))dx =∫_0 ^π cosx dx−6∫_0 ^π ((cosx)/(7−sin^2 x))dx we have ∫_0 ^π cosx dx=[sinx]_0 ^π =0 and ∫_0 ^π ((cosxdx)/(7−sin^2 x))=∫_0 ^(π/2) ((cosx)/(7−sin^2 x))dx +∫_(π/2) ^π ((cosx)/(7−sin^2 x))(→x=(π/2)+t) =_(sinx=y) ∫_0 ^1 (dy/(7−y^2 )) +∫_0 ^(π/2) ((−sint dt)/(7−cos^2 t))(→cost=y) =∫_0 ^1 (dy/(7−y^2 )) −∫_0 ^1 (dy/(7−y^2 )) =0 ⇒Ψ=0](https://www.tinkutara.com/question/Q149115.png)
$$\Psi=\int_{\mathrm{0}} ^{\pi\:} \:\frac{\mathrm{cos}^{\mathrm{3}} \mathrm{x}}{\mathrm{7}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:\Rightarrow\Psi=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cos}^{\mathrm{3}} \mathrm{x}}{\mathrm{7}−\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cos}^{\mathrm{3}} \mathrm{x}}{\mathrm{6}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cosx}\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{6}\right)−\mathrm{6cosx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:+\mathrm{6}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\mathrm{cosx}\:\mathrm{dx}−\mathrm{6}\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cosx}}{\mathrm{7}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{cosx}\:\mathrm{dx}=\left[\mathrm{sinx}\right]_{\mathrm{0}} ^{\pi} =\mathrm{0}\:\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cosxdx}}{\mathrm{7}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{cosx}}{\mathrm{7}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\frac{\mathrm{cosx}}{\mathrm{7}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\left(\rightarrow\mathrm{x}=\frac{\pi}{\mathrm{2}}+\mathrm{t}\right) \\ $$$$=_{\mathrm{sinx}=\mathrm{y}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dy}}{\mathrm{7}−\mathrm{y}^{\mathrm{2}} }\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{−\mathrm{sint}\:\mathrm{dt}}{\mathrm{7}−\mathrm{cos}^{\mathrm{2}} \mathrm{t}}\left(\rightarrow\mathrm{cost}=\mathrm{y}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dy}}{\mathrm{7}−\mathrm{y}^{\mathrm{2}} }\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dy}}{\mathrm{7}−\mathrm{y}^{\mathrm{2}} }\:=\mathrm{0}\:\Rightarrow\Psi=\mathrm{0} \\ $$
Commented by bramlexs22 last updated on 03/Aug/21

$$\mathrm{yes}.\:\mathrm{thanks} \\ $$
Commented by ArielVyny last updated on 04/Aug/21
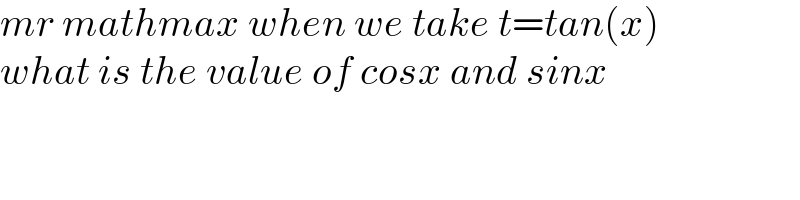
$${mr}\:{mathmax}\:{when}\:{we}\:{take}\:{t}={tan}\left({x}\right) \\ $$$${what}\:{is}\:{the}\:{value}\:{of}\:{cosx}\:{and}\:{sinx} \\ $$
