Question Number 34992 by MJS last updated on 14/May/18
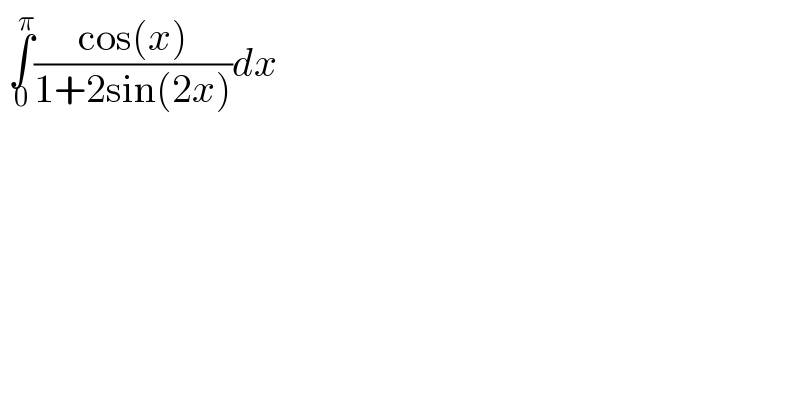
$$\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{cos}\left({x}\right)}{\mathrm{1}+\mathrm{2sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$
Commented by math khazana by abdo last updated on 14/May/18
![let put I = ∫_0 ^π ((cosx)/(1+2sin(2x)))dx I = ∫_0 ^π ((cosx)/(1+4cosx sinx))dx .changement tan((x/2))=t give I = ∫_0 ^∞ (((1−t^2 )/(1+t^2 ))/(1+4 ((1−t^2 )/(1+t^2 )) ((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) = 2∫_0 ^∞ ((1−t^2 )/((1+t^2 )^2 ( 1+((8t(1−t^2 ))/((1+t^2 )^2 )))))dt = 2 ∫_0 ^∞ ((1−t^2 )/((1+t^2 )^2 +8t(1−t^2 )))dt = 2 ∫_0 ^∞ ((1−t^2 )/(t^4 +2t^2 +1 +8t −8t^3 ))dt = 2 ∫_0 ^∞ ((1−t^2 )/(t^4 −8t^3 +2t^2 +8t +1))dt let drcompose F(t) = ((1−t^2 )/(t^4 −8t^3 +2t^2 +8t +1)) the roots of p(t)=t^4 −8t^3 +2t^2 +8t +1 are t_1 ∼7,59 t_2 ∼1,3 t_3 ∼−0,76 t_4 ∼−0,13 ⇒ F(t) = ((1−t^2 )/((t −t_1 )(t −t_2 )(t −t_3 )(t −t_4 ))) = (a/(t−t_1 )) +(b/(t−t_2 )) +(c/(t−t_3 )) +(d/(t −t_4 )) a=lim_(t→t_1 ) (t−t_1 )F(t)= ((1−t_1 ^2 )/((t_1 −t_2 )(t_1 −t_3 )(t_1 −t_4 ))) =ξ(t_1 ) (1−t_1 ^2 ) with ξ(t_1 )= (1/((t_1 −t_2 )(t_1 −t_3 )(t_1 −t_4 ))) b =ξ(t_2 )(1−t_2 ^2 ) with ξ(t_2 )= (1/((t_2 −t_1 )(t_2 −t_3 )(t_2 −t_4 ))) c =ξ(t_3 )(1−t_3 ^2 ) d=ξ(t_4 )(1−t_4 ^2 ) ⇒ I =2 ∫_0 ^∞ F(t)dt = 2 [ aln∣t−t_1 ∣ +b ln∣t−t_2 ∣ +c ln∣t−t_3 ) +d ln∣t−t_4 ∣]_0 ^(+∞) =2[ ln∣(((t−t_1 )a)/((t −t_2 )^b )) ∣ + ln∣ (((t−t_3 )^c )/((t−t_4 )^d ))∣]_0 ^(+∞) =2{−ln∣(((−t_1 )^a )/((−t_2 )^b )) ∣−ln∣(((−t_3 )^c )/((−t_4 )^d ))∣} =2{ bln∣t_2 ∣ −aln∣t_1 ∣ +dln∣t_4 ∣ −c ln∣t_3 ∣}... the approximate value of I isdetermined...](https://www.tinkutara.com/question/Q35031.png)
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{cosx}}{\mathrm{1}+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{cosx}}{\mathrm{1}+\mathrm{4}{cosx}\:{sinx}}{dx}\:\:.{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t} \\ $$$${give}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{4}\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\:\:\mathrm{1}+\frac{\mathrm{8}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)}{dt} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:\:+\mathrm{8}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\:+\mathrm{8}{t}\:−\mathrm{8}{t}^{\mathrm{3}} }{dt} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:−\mathrm{8}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{8}{t}\:+\mathrm{1}}{dt}\:\:{let}\:{drcompose} \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:−\mathrm{8}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{8}{t}\:+\mathrm{1}} \\ $$$${the}\:{roots}\:{of}\:{p}\left({t}\right)={t}^{\mathrm{4}} \:−\mathrm{8}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{8}{t}\:+\mathrm{1}\:{are} \\ $$$${t}_{\mathrm{1}} \:\sim\mathrm{7},\mathrm{59}\:\:\:\:\:\:{t}_{\mathrm{2}} \sim\mathrm{1},\mathrm{3}\:\:\:\:\:{t}_{\mathrm{3}} \sim−\mathrm{0},\mathrm{76}\:\:\:{t}_{\mathrm{4}} \sim−\mathrm{0},\mathrm{13}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left({t}\:−{t}_{\mathrm{1}} \right)\left({t}\:−{t}_{\mathrm{2}} \right)\left({t}\:−{t}_{\mathrm{3}} \right)\left({t}\:−{t}_{\mathrm{4}} \right)} \\ $$$$=\:\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:+\frac{{c}}{{t}−{t}_{\mathrm{3}} }\:+\frac{{d}}{{t}\:−{t}_{\mathrm{4}} } \\ $$$${a}={lim}_{{t}\rightarrow{t}_{\mathrm{1}} } \left({t}−{t}_{\mathrm{1}} \right){F}\left({t}\right)=\:\frac{\mathrm{1}−{t}_{\mathrm{1}} ^{\mathrm{2}} }{\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)\left({t}_{\mathrm{1}} \:−{t}_{\mathrm{3}} \right)\left({t}_{\mathrm{1}} \:−{t}_{\mathrm{4}} \right)} \\ $$$$=\xi\left({t}_{\mathrm{1}} \right)\:\left(\mathrm{1}−{t}_{\mathrm{1}} ^{\mathrm{2}} \right)\:\:{with}\:\xi\left({t}_{\mathrm{1}} \right)=\:\frac{\mathrm{1}}{\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)\left({t}_{\mathrm{1}} −{t}_{\mathrm{3}} \right)\left({t}_{\mathrm{1}} −{t}_{\mathrm{4}} \right)} \\ $$$${b}\:=\xi\left({t}_{\mathrm{2}} \right)\left(\mathrm{1}−{t}_{\mathrm{2}} ^{\mathrm{2}} \right)\:{with}\:\xi\left({t}_{\mathrm{2}} \right)=\:\frac{\mathrm{1}}{\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)\left({t}_{\mathrm{2}} −{t}_{\mathrm{3}} \right)\left({t}_{\mathrm{2}} −{t}_{\mathrm{4}} \right)} \\ $$$${c}\:=\xi\left({t}_{\mathrm{3}} \right)\left(\mathrm{1}−{t}_{\mathrm{3}} ^{\mathrm{2}} \right) \\ $$$${d}=\xi\left({t}_{\mathrm{4}} \right)\left(\mathrm{1}−{t}_{\mathrm{4}} ^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${I}\:\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} {F}\left({t}\right){dt} \\ $$$$\left.\:=\:\mathrm{2}\:\left[\:{aln}\mid{t}−{t}_{\mathrm{1}} \mid\:+{b}\:{ln}\mid{t}−{t}_{\mathrm{2}} \mid\:+{c}\:{ln}\mid{t}−{t}_{\mathrm{3}} \right)\:+{d}\:{ln}\mid{t}−{t}_{\mathrm{4}} \mid\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\mathrm{2}\left[\:{ln}\mid\frac{\left({t}−{t}_{\mathrm{1}} \right){a}}{\left({t}\:−{t}_{\mathrm{2}} \right)^{{b}} }\:\mid\:+\:{ln}\mid\:\frac{\left({t}−{t}_{\mathrm{3}} \right)^{{c}} }{\left({t}−{t}_{\mathrm{4}} \right)^{{d}} }\mid\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\mathrm{2}\left\{−{ln}\mid\frac{\left(−{t}_{\mathrm{1}} \right)^{{a}} }{\left(−{t}_{\mathrm{2}} \right)^{{b}} }\:\mid−{ln}\mid\frac{\left(−{t}_{\mathrm{3}} \right)^{{c}} }{\left(−{t}_{\mathrm{4}} \right)^{{d}} }\mid\right\} \\ $$$$=\mathrm{2}\left\{\:{bln}\mid{t}_{\mathrm{2}} \mid\:−{aln}\mid{t}_{\mathrm{1}} \mid\:\:+{dln}\mid{t}_{\mathrm{4}} \mid\:−{c}\:{ln}\mid{t}_{\mathrm{3}} \mid\right\}… \\ $$$${the}\:{approximate}\:{value}\:{of}\:{I}\:{isdetermined}… \\ $$$$ \\ $$
Answered by MJS last updated on 14/May/18
![∫_0 ^π ((cos(x))/(1+2sin(2x)))dx=∫_(−(π/2)) ^(π/2) ((sin(x))/(2sin(2x)−1))dx= =∫_(−(π/2)) ^(π/2) ((sin(x))/(4sin(x)cos(x)−1))dx= [((t=tan((x/2)) → dx=((2dt)/(t^2 +1)))),((sin(x)=((2t)/(t^2 +1)); cos(x)=−((t^2 −1)/(t^2 +1)))) ] =−4∫_(−1) ^1 (t/(t^4 +8t^3 +2t^2 −8t+1))dt= [((t^4 +8t^3 +2t^2 −8t+1=0)),((t_1 =−2−(√6)−(√3)−(√2))),((t_2 =−2−(√6)+(√3)+(√2))),((t_3 =−2+(√6)−(√3)+(√2))),((t_4 =−2+(√6)+(√3)−(√2))) ] =−4∫_(−1) ^1 ((A/(t−t_1 ))+(B/(t−t_2 ))+(C/(t−t_3 ))+(D/(t−t_4 )))dt= =−4[Aln∣t−t_1 ∣+Bln∣t−t_2 ∣+Cln∣t−t_3 ∣+Dln∣t−t_4 ∣]_(−1) ^1 = =−4[Aln∣tan((x/2))−t_1 ∣+Bln∣tan((x/2))−t_2 ∣+Cln∣tan((x/2))−t_3 ∣+Dln∣tan((x/2))−t_4 ∣]_(−(π/2)) ^(π/2) = [((A=(t_1 /((t_1 −t_2 )(t_1 −t_3 )(t_1 −t_4 )))=((−(√6)+3(√2))/(96)))),((B=(t_2 /((t_2 −t_1 )(t_2 −t_3 )(t_2 −t_4 )))=((−(√6)−3(√2))/(96)))),((C=(t_3 /((t_3 −t_1 )(t_3 −t_2 )(t_3 −t_4 )))=(((√6)−3(√2))/(96)))),((D=(t_4 /((t_4 −t_1 )(t_4 −t_2 )(t_4 −t_3 )))=(((√6)+3(√2))/(96)))) ] =−(1/(24))[(−(√6)+3(√2))ln∣tan((x/2))+2+(√6)+(√3)+(√2)∣+(−(√6)−3(√2))ln∣tan((x/2))+2+(√6)−(√3)−(√2)∣+((√6)−3(√2))ln∣tan((x/2))+2−(√6)+(√3)−(√2)∣+((√6)+3(√2))ln∣tan((x/2))+2−(√6)−(√3)+(√2)∣]_(−(π/2)) ^(π/2) ≈ ≈1.091166](https://www.tinkutara.com/question/Q34995.png)
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{cos}\left({x}\right)}{\mathrm{1}+\mathrm{2sin}\left(\mathrm{2}{x}\right)}{dx}=\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}\left({x}\right)}{\mathrm{2sin}\left(\mathrm{2}{x}\right)−\mathrm{1}}{dx}= \\ $$$$=\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}\left({x}\right)}{\mathrm{4sin}\left({x}\right)\mathrm{cos}\left({x}\right)−\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\begin{bmatrix}{{t}=\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}}\\{\mathrm{sin}\left({x}\right)=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}};\:\mathrm{cos}\left({x}\right)=−\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}}\end{bmatrix} \\ $$$$=−\mathrm{4}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\frac{{t}}{{t}^{\mathrm{4}} +\mathrm{8}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\begin{bmatrix}{{t}^{\mathrm{4}} +\mathrm{8}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{1}=\mathrm{0}}\\{{t}_{\mathrm{1}} =−\mathrm{2}−\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}\\{{t}_{\mathrm{2}} =−\mathrm{2}−\sqrt{\mathrm{6}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}}\\{{t}_{\mathrm{3}} =−\mathrm{2}+\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}}\\{{t}_{\mathrm{4}} =−\mathrm{2}+\sqrt{\mathrm{6}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}\end{bmatrix} \\ $$$$=−\mathrm{4}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\left(\frac{\mathcal{A}}{{t}−{t}_{\mathrm{1}} }+\frac{\mathcal{B}}{{t}−{t}_{\mathrm{2}} }+\frac{\mathcal{C}}{{t}−{t}_{\mathrm{3}} }+\frac{\mathcal{D}}{{t}−{t}_{\mathrm{4}} }\right){dt}= \\ $$$$=−\mathrm{4}\left[\mathcal{A}\mathrm{ln}\mid{t}−{t}_{\mathrm{1}} \mid+\mathcal{B}\mathrm{ln}\mid{t}−{t}_{\mathrm{2}} \mid+\mathcal{C}\mathrm{ln}\mid{t}−{t}_{\mathrm{3}} \mid+\mathcal{D}\mathrm{ln}\mid{t}−{t}_{\mathrm{4}} \mid\right]_{−\mathrm{1}} ^{\mathrm{1}} = \\ $$$$=−\mathrm{4}\left[\mathcal{A}\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{t}_{\mathrm{1}} \mid+\mathcal{B}\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{t}_{\mathrm{2}} \mid+\mathcal{C}\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{t}_{\mathrm{3}} \mid+\mathcal{D}\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{t}_{\mathrm{4}} \mid\overset{\frac{\pi}{\mathrm{2}}} {\right]}_{−\frac{\pi}{\mathrm{2}}} = \\ $$$$\:\:\:\:\:\:\:\:\:\:\begin{bmatrix}{\mathcal{A}=\frac{{t}_{\mathrm{1}} }{\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)\left({t}_{\mathrm{1}} −{t}_{\mathrm{3}} \right)\left({t}_{\mathrm{1}} −{t}_{\mathrm{4}} \right)}=\frac{−\sqrt{\mathrm{6}}+\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{96}}}\\{\mathcal{B}=\frac{{t}_{\mathrm{2}} }{\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)\left({t}_{\mathrm{2}} −{t}_{\mathrm{3}} \right)\left({t}_{\mathrm{2}} −{t}_{\mathrm{4}} \right)}=\frac{−\sqrt{\mathrm{6}}−\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{96}}}\\{\mathcal{C}=\frac{{t}_{\mathrm{3}} }{\left({t}_{\mathrm{3}} −{t}_{\mathrm{1}} \right)\left({t}_{\mathrm{3}} −{t}_{\mathrm{2}} \right)\left({t}_{\mathrm{3}} −{t}_{\mathrm{4}} \right)}=\frac{\sqrt{\mathrm{6}}−\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{96}}}\\{\mathcal{D}=\frac{{t}_{\mathrm{4}} }{\left({t}_{\mathrm{4}} −{t}_{\mathrm{1}} \right)\left({t}_{\mathrm{4}} −{t}_{\mathrm{2}} \right)\left({t}_{\mathrm{4}} −{t}_{\mathrm{3}} \right)}=\frac{\sqrt{\mathrm{6}}+\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{96}}}\end{bmatrix} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{24}}\left[\left(−\sqrt{\mathrm{6}}+\mathrm{3}\sqrt{\mathrm{2}}\right)\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}+\sqrt{\mathrm{6}}+\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\mid+\left(−\sqrt{\mathrm{6}}−\mathrm{3}\sqrt{\mathrm{2}}\right)\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}+\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\mid+\left(\sqrt{\mathrm{6}}−\mathrm{3}\sqrt{\mathrm{2}}\right)\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}−\sqrt{\mathrm{6}}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\mid+\left(\sqrt{\mathrm{6}}+\mathrm{3}\sqrt{\mathrm{2}}\right)\mathrm{ln}\mid\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}−\sqrt{\mathrm{6}}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\mid\overset{\frac{\pi}{\mathrm{2}}} {\right]}_{−\frac{\pi}{\mathrm{2}}} \approx \\ $$$$\approx\mathrm{1}.\mathrm{091166} \\ $$
Commented by MJS last updated on 14/May/18

$$\mathrm{I}\:\mathrm{couldn}'\mathrm{t}\:\mathrm{get}\:\mathrm{this}\:\mathrm{out}\:\mathrm{of}\:\mathrm{my}\:\mathrm{head}… \\ $$$$\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:\mathrm{the}\:\mathrm{solution},\:\mathrm{please}\:\mathrm{check}\:\mathrm{for} \\ $$$$\mathrm{mistakes}\:\mathrm{of}\:\mathrm{method}. \\ $$$$\mathrm{I}\:\mathrm{can}\:\mathrm{guarantee}\:\mathrm{the}\:\mathrm{correctness}\:\mathrm{of}\:\mathrm{the}\:\mathrm{zeros} \\ $$$${t}_{\mathrm{1}} ,\:{t}_{\mathrm{2}} ,\:{t}_{\mathrm{3}} ,\:{t}_{\mathrm{4}} \:\mathrm{and}\:\mathrm{the}\:\mathrm{coefficients}\:\mathcal{A},\:\mathcal{B},\:\mathcal{C},\:\mathcal{D}. \\ $$
Commented by ajfour last updated on 14/May/18
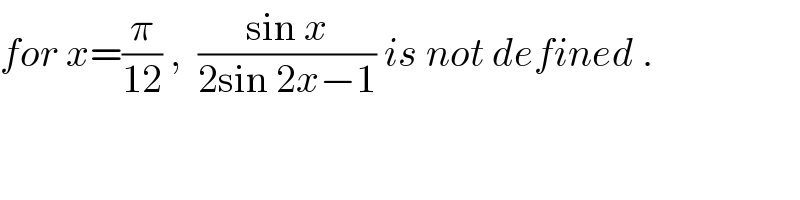
$${for}\:{x}=\frac{\pi}{\mathrm{12}}\:,\:\:\frac{\mathrm{sin}\:{x}}{\mathrm{2sin}\:\mathrm{2}{x}−\mathrm{1}}\:{is}\:{not}\:{defined}\:. \\ $$
Commented by MJS last updated on 14/May/18
![but it′s the Cauchy principal value: ∫(p/(x−q))dx=pln∣x−q∣ a<q<b; h>0 ∫_a ^b (p/(x−q))dx=lim_(h→0) (∫_a ^(q−h) (p/(x−q))dx+∫_(q+h) ^b (p/(x−q))dx)= =lim_(h→0) ([pln∣x−q∣]_a ^(q−h) +[pln∣x−q∣]_(q+h) ^b )= =lim_(h→0) (pln∣h∣−pln∣a−q∣+pln∣b−q∣−pln∣h∣)= =lim_(h→0) (pln∣b−q∣−pln∣a−q∣)= =pln∣b−q∣−pln∣a−q∣=∫_a ^b (p/(x−q))dx q.e.d.](https://www.tinkutara.com/question/Q35020.png)
$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{Cauchy}\:\mathrm{principal}\:\mathrm{value}: \\ $$$$\int\frac{{p}}{{x}−{q}}{dx}={p}\mathrm{ln}\mid{x}−{q}\mid \\ $$$${a}<{q}<{b};\:{h}>\mathrm{0} \\ $$$$\underset{{a}} {\overset{{b}} {\int}}\frac{{p}}{{x}−{q}}{dx}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\underset{{a}} {\overset{{q}−{h}} {\int}}\frac{{p}}{{x}−{q}}{dx}+\underset{{q}+{h}} {\overset{{b}} {\int}}\frac{{p}}{{x}−{q}}{dx}\right)= \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\left[{p}\mathrm{ln}\mid{x}−{q}\mid\right]_{{a}} ^{{q}−{h}} +\left[{p}\mathrm{ln}\mid{x}−{q}\mid\right]_{{q}+{h}} ^{{b}} \right)= \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({p}\mathrm{ln}\mid{h}\mid−{p}\mathrm{ln}\mid{a}−{q}\mid+{p}\mathrm{ln}\mid{b}−{q}\mid−{p}\mathrm{ln}\mid{h}\mid\right)= \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({p}\mathrm{ln}\mid{b}−{q}\mid−{p}\mathrm{ln}\mid{a}−{q}\mid\right)= \\ $$$$={p}\mathrm{ln}\mid{b}−{q}\mid−{p}\mathrm{ln}\mid{a}−{q}\mid=\underset{{a}} {\overset{{b}} {\int}}\frac{{p}}{{x}−{q}}{dx} \\ $$$${q}.{e}.{d}. \\ $$
Commented by ajfour last updated on 14/May/18
$${not}\:{as}\:{sure},\:{you}\:{know}\:{better}. \\ $$
