Question Number 107051 by Ar Brandon last updated on 08/Aug/20
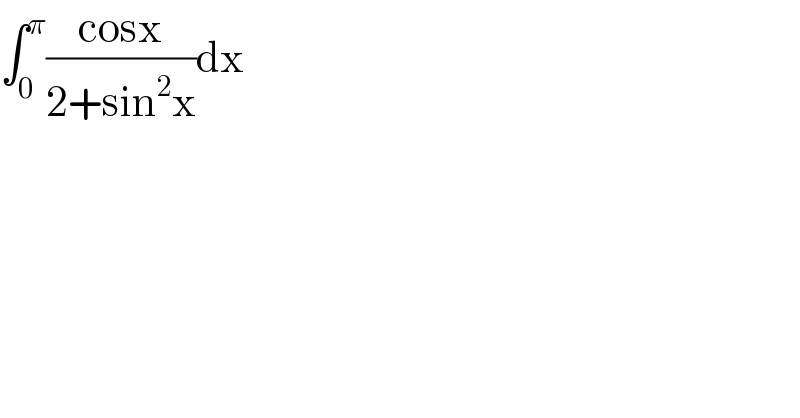
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{cosx}}{\mathrm{2}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Aug/20
![∫_0 ^π (dt/(2+t^2 )) (sinx=t) (1/( (√2)))tan^(−1) ((t/( (√2))))+C=[(1/( (√2)))tan^(−1) (((sinx)/( (√2))))]_0 ^π =0](https://www.tinkutara.com/question/Q107054.png)
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dt}}{\mathrm{2}+\mathrm{t}^{\mathrm{2}} }\:\:\left(\mathrm{sinx}=\mathrm{t}\right) \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{t}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C}=\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sinx}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\pi} =\mathrm{0} \\ $$
Commented by Ar Brandon last updated on 08/Aug/20
OK, I got it now��
Commented by Dwaipayan Shikari last updated on 08/Aug/20
��
Answered by Ar Brandon last updated on 08/Aug/20
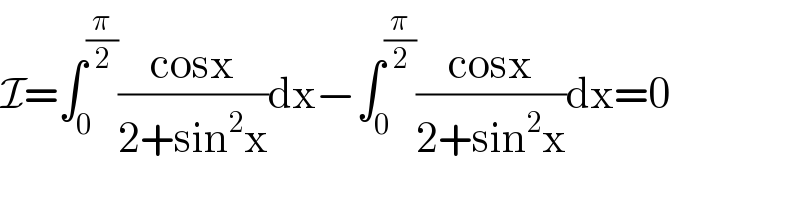
$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cosx}}{\mathrm{2}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cosx}}{\mathrm{2}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}=\mathrm{0} \\ $$
