Question Number 63927 by aliesam last updated on 11/Jul/19
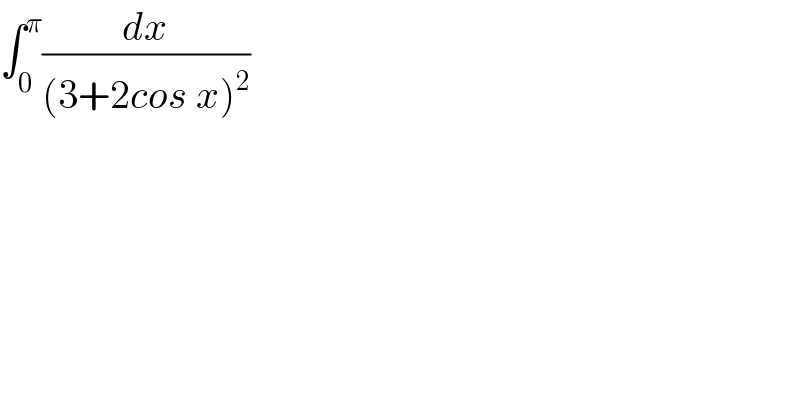
$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left(\mathrm{3}+\mathrm{2}{cos}\:{x}\right)^{\mathrm{2}} } \\ $$
Commented by aliesam last updated on 12/Jul/19

$${god}\:{bless}\:{you}\:{sir}\:..{well}\:{done}.. \\ $$
Commented by mathmax by abdo last updated on 12/Jul/19
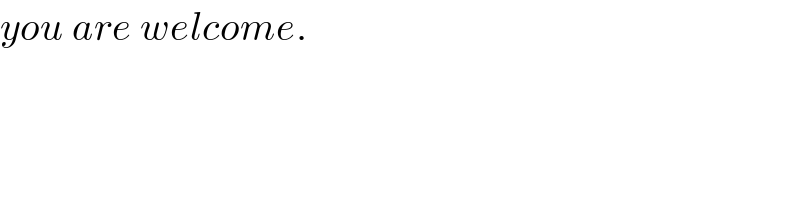
$${you}\:{are}\:{welcome}. \\ $$
Commented by aliesam last updated on 11/Jul/19

$${thank}\:{you}\:{sir}\: \\ $$
Commented by aliesam last updated on 11/Jul/19
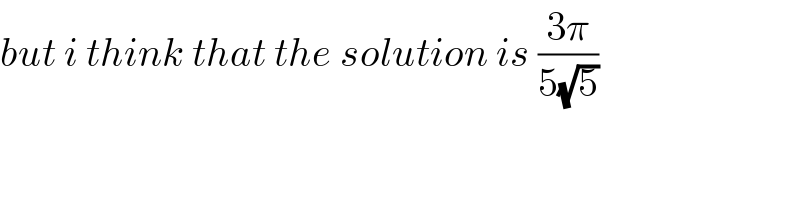
$${but}\:{i}\:{think}\:{that}\:{the}\:{solution}\:{is}\:\frac{\mathrm{3}\pi}{\mathrm{5}\sqrt{\mathrm{5}}} \\ $$
Commented by mathmax by abdo last updated on 12/Jul/19

$${let}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{{t}+\mathrm{2}{cosx}}\:\Rightarrow{f}^{'} \left({t}\right)\:=−\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{\left({t}+\mathrm{2}{cosx}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{\left({t}+\mathrm{2}{cosx}\right)^{\mathrm{2}} }\:=−{f}^{'} \left({t}\right)\:{and}\:\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{\left(\mathrm{3}+\mathrm{2}{cosx}\right)^{\mathrm{2}} }\:=−{f}^{'} \left(\mathrm{3}\right) \\ $$$${let}\:{calculate}\:{f}\left({t}\right)\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={u}\:{give} \\ $$$${f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\:{t}\:+\mathrm{2}\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{du}}{{t}+{tu}^{\mathrm{2}} \:+\mathrm{2}−\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{du}}{\left({t}−\mathrm{2}\right){u}^{\mathrm{2}} \:+{t}+\mathrm{2}}\:\:{due}\:{to}\:{our}\:{case}\:{we}\:{take}\:{t}>\mathrm{2}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\frac{\mathrm{2}}{\left({t}−\mathrm{2}\right)}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\frac{{t}+\mathrm{2}}{{t}−\mathrm{2}}}\:=_{{u}=\sqrt{\frac{{t}+\mathrm{2}}{{t}−\mathrm{2}}}\alpha} \:\:\frac{\mathrm{2}}{{t}−\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\frac{{t}+\mathrm{2}}{{t}−\mathrm{2}}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\sqrt{\frac{{t}+\mathrm{2}}{{t}−\mathrm{2}}}{d}\alpha \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}}\:\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{{t}^{\mathrm{2}} \:−\mathrm{4}}}\:\Rightarrow{f}^{'} \left({t}\right)\:=\pi\left\{\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=−\frac{\pi}{\mathrm{2}}\left(\mathrm{2}{t}\right)\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:=\frac{−\pi{t}}{\left({t}^{\mathrm{2}} −\mathrm{4}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dx}}{\left({t}+\mathrm{2}{cosx}\right)^{\mathrm{2}} }\:=\frac{\pi{t}}{\left({t}^{\mathrm{2}} −\mathrm{4}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}}\:\:{and} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{\left(\mathrm{3}+\mathrm{2}{cosx}\right)^{\mathrm{2}} }\:=\frac{\mathrm{3}\pi}{\left(\mathrm{9}−\mathrm{4}\right)\sqrt{\mathrm{9}−\mathrm{4}}}\:=\frac{\mathrm{3}\pi}{\mathrm{5}\sqrt{\mathrm{5}}}\:. \\ $$
Commented by aliesam last updated on 11/Jul/19

Commented by aliesam last updated on 11/Jul/19

