Question Number 105706 by bramlex last updated on 31/Jul/20
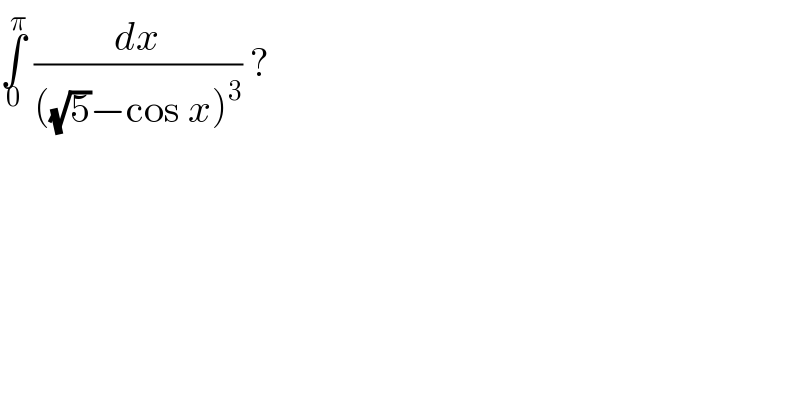
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{dx}}{\left(\sqrt{\mathrm{5}}−\mathrm{cos}\:{x}\right)^{\mathrm{3}} }\:? \\ $$
Answered by john santu last updated on 31/Jul/20
![F(a) = ∫_0 ^π (dx/(a−cos x)) = (π/( (√(a^2 −1)))) F ′(a) = ∫ (∂/∂a)[(dx/(a−cos x)) ] = (∂/∂a) [(π/( (√(a^2 −1))))] −∫_0 ^π ((dx/((a−cos x)^2 )))=−πa^2 (a^2 −1)^(−3/2) F ′′(a)= ∫_0 ^π (∂/∂a)[(dx/((a−cos x)^2 ))]=−π[(a^2 −1)^(−3/2) −3a^2 (a^2 −1)^(−5/2) ] ∫_0 ^π (dx/((1−cos x)^3 )) = −(π/2)(a^2 −1)^(−5/2) ((a^2 −1)−3a^2 ) = (π/2). ((2a^2 +1)/((a^2 −1)^(5/2) )) put a = (√5) ∫_0 ^π (dx/(((√5)−cos x)^3 )) = ((11π)/(64)) . ★](https://www.tinkutara.com/question/Q105709.png)
$${F}\left({a}\right)\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{dx}}{{a}−\mathrm{cos}\:{x}}\:=\:\frac{\pi}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${F}\:'\left({a}\right)\:=\:\int\:\frac{\partial}{\partial{a}}\left[\frac{{dx}}{{a}−\mathrm{cos}\:{x}}\:\right]\:=\:\frac{\partial}{\partial{a}}\:\left[\frac{\pi}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\right] \\ $$$$−\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\left(\frac{{dx}}{\left({a}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\right)=−\pi{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −\mathrm{1}\right)^{−\mathrm{3}/\mathrm{2}} \\ $$$${F}\:''\left({a}\right)=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\partial}{\partial{a}}\left[\frac{{dx}}{\left({a}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\right]=−\pi\left[\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{−\mathrm{3}/\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −\mathrm{1}\right)^{−\mathrm{5}/\mathrm{2}} \right] \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{dx}}{\left(\mathrm{1}−\mathrm{cos}\:{x}\right)^{\mathrm{3}} }\:=\:−\frac{\pi}{\mathrm{2}}\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{−\mathrm{5}/\mathrm{2}} \left(\left({a}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{3}{a}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{2}}.\:\frac{\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}}{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{5}/\mathrm{2}} } \\ $$$${put}\:{a}\:=\:\sqrt{\mathrm{5}} \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{dx}}{\left(\sqrt{\mathrm{5}}−\mathrm{cos}\:{x}\right)^{\mathrm{3}} }\:=\:\frac{\mathrm{11}\pi}{\mathrm{64}}\:.\:\bigstar \\ $$
