Menu Close

0-pi-dx-a-2-cos-2-x-b-2-sin-2-x-

Tinku Tara 0 Comments
Pin




Question Number 91892 by john santu last updated on 03/May/20
∫_0 ^π (dx/(a^2 cos^2 x+b^2 sin^2 x)) ?
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{dx}}{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {x}+{b}^{\mathrm{2}} \:\mathrm{sin}\:^{\mathrm{2}} {x}}\:? \\ $$
Commented by john santu last updated on 03/May/20
∫ (dx/((b^2 −a^2 )sin^2 x+a^2 )) say a^2 = p ∧ b^2 −a^2 =q ∫ (dx/(q sin^2 x+p)) = Wierstrass let tan ((x/2))=t dx = ((2t )/(1+t^2 )) dt tobe continue
$$\int\:\frac{{dx}}{\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\mathrm{sin}\:^{\mathrm{2}} {x}+{a}^{\mathrm{2}} } \\ $$$${say}\:{a}^{\mathrm{2}} =\:{p}\:\wedge\:{b}^{\mathrm{2}} −{a}^{\mathrm{2}} ={q} \\ $$$$\int\:\frac{{dx}}{{q}\:\mathrm{sin}\:^{\mathrm{2}} {x}+{p}}\:= \\ $$$${W}\mathrm{ierstrass}\:\mathrm{let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)=\mathrm{t}\: \\ $$$${dx}\:=\:\frac{\mathrm{2t}\:}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt} \\ $$$$\mathrm{tobe}\:\mathrm{continue} \\ $$
Commented by Prithwish Sen 1 last updated on 03/May/20
∫_0 ^π ((sec^2 x dx)/(a^2 +b^2 tan^2 x)) = (1/(ab))[tan^(−1) (((btan x)/a))]_0 ^π
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:\:=\:\frac{\mathrm{1}}{\mathrm{ab}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{btan}\:\mathrm{x}}{\mathrm{a}}\right)\right]_{\mathrm{0}} ^{\pi} \\ $$
Commented by mathmax by abdo last updated on 03/May/20
I =∫_0 ^π (dx/(a^2 cos^2 x +b^2 sin^2 x)) ⇒I =∫_0 ^π ((2dx)/(a^2 (1+cos(2x))+b^2 (1−cos(2x)))) =∫_0 ^π ((2dx)/(a^2 +b^2 +(a^2 −b^2 )cos(2x))) =_(2x=t) ∫_0 ^(2π) (dt/(a^2 +b^2 +(a^2 −b^2 )cost)) =_(e^(it) =z) ∫_(∣z∣=1) (dz/(iz(a^2 +b^2 +(a^2 −b^2 )×((z+z^(−1) )/2)))) =∫_(∣z∣=1) ((2dz)/(iz{2(a^2 +b^2 )+(a^2 −b^2 )(z+z^(−1) )})) =∫ ((−2i dz)/(2(a^2 +b^2 )z +(a^2 −b^2 )z^2 +a^2 −b^2 )) let ϕ(z) =((−2i)/((a^2 −b^2 )z^2 +2(a^2 +b^2 )z +a^2 −b^2 )) poles of ϕ? Δ^′ =(a^2 +b^2 )^2 −(a^2 −b^2 )^2 =a^4 +b^4 +2a^2 b^2 −a^4 −b^4 +2a^2 b^2 =4a^2 b^2 ⇒ z_1 =((−(a^2 +b^2 )+2∣ab∣)/(a^2 −b^2 ))=−(((∣a∣−∣b∣)^2 )/(∣a∣^2 −∣b∣^2 ))=−((∣a∣−∣b∣)/(∣a∣+∣b∣)) (we suppose a≠b) z_2 =((−(a^2 +b^2 )−2∣ab∣)/(a^2 −b^2 )) =−((∣a∣+∣b∣)/(∣a∣−∣b∣)) =(1/z_1 ) ∣z_1 ∣−1 =((∣∣a∣−∣b∣∣)/(∣a∣+∣b∣))−1 <0 because ∣....∣≤∣a∣ +∣b∣ ⇒∣z_2 ∣−1>0 ⇒ (z_2 is out of circle) ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_1 ) ϕ(z) =((−2i)/((a^2 −b^2 )(z−z_1 )(z−z_2 ))) ⇒Res(ϕ,z_1 ) =((−2i)/((a^2 −b^2 )(z_1 −z_2 ))) =((−2i)/((a^2 −b^2 )×((4∣ab∣)/(a^2 −b^2 )))) =((−i)/(2∣ab∣)) ⇒∫_(∣z∣=1) ϕ(z) dz =((2iπ×(−i))/(2∣ab∣)) =(π/(∣ab∣)) ⇒ I =(π/(∣a∣×∣b∣)) (ab≠0) if a=b ≠0 ⇒ I = ∫_0 ^π (dx/(a^2 )) =(π/a^2 )
$${I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{{a}^{\mathrm{2}} \:{cos}^{\mathrm{2}} {x}\:+{b}^{\mathrm{2}} \:{sin}^{\mathrm{2}} {x}}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{2}{dx}}{{a}^{\mathrm{2}} \left(\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)\right)+{b}^{\mathrm{2}} \left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right)} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{2}{dx}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cos}\left(\mathrm{2}{x}\right)}\:=_{\mathrm{2}{x}={t}} \:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dt}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cost}} \\ $$$$=_{{e}^{{it}} \:={z}} \:\:\:\:\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\:\:\:\frac{{dz}}{{iz}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)×\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}\right)} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{2}{dz}}{{iz}\left\{\mathrm{2}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({z}+{z}^{−\mathrm{1}} \right)\right\}} \\ $$$$=\int\:\:\frac{−\mathrm{2}{i}\:{dz}}{\mathrm{2}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right){z}\:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){z}^{\mathrm{2}} \:+{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:{let}\: \\ $$$$\varphi\left({z}\right)\:=\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){z}^{\mathrm{2}} \:+\mathrm{2}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right){z}\:+{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\:{poles}\:{of}\:\varphi? \\ $$$$\Delta^{'} \:=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \:={a}^{\mathrm{4}} \:+{b}^{\mathrm{4}} \:+\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −{a}^{\mathrm{4}} −{b}^{\mathrm{4}} \:+\mathrm{2}{a}^{\mathrm{2}} \:{b}^{\mathrm{2}} \\ $$$$=\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\Rightarrow\:{z}_{\mathrm{1}} =\frac{−\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)+\mathrm{2}\mid{ab}\mid}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }=−\frac{\left(\mid{a}\mid−\mid{b}\mid\right)^{\mathrm{2}} }{\mid{a}\mid^{\mathrm{2}} −\mid{b}\mid^{\mathrm{2}} }=−\frac{\mid{a}\mid−\mid{b}\mid}{\mid{a}\mid+\mid{b}\mid}\:\:\:\:\left({we}\:{suppose}\:{a}\neq{b}\right) \\ $$$${z}_{\mathrm{2}} =\frac{−\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)−\mathrm{2}\mid{ab}\mid}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:=−\frac{\mid{a}\mid+\mid{b}\mid}{\mid{a}\mid−\mid{b}\mid}\:=\frac{\mathrm{1}}{{z}_{\mathrm{1}} } \\ $$$$\mid{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\frac{\mid\mid{a}\mid−\mid{b}\mid\mid}{\mid{a}\mid+\mid{b}\mid}−\mathrm{1}\:<\mathrm{0}\:{because}\:\mid….\mid\leqslant\mid{a}\mid\:+\mid{b}\mid\:\Rightarrow\mid{z}_{\mathrm{2}} \mid−\mathrm{1}>\mathrm{0}\:\Rightarrow \\ $$$$\left({z}_{\mathrm{2}} {is}\:{out}\:{of}\:{circle}\right) \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right) \\ $$$$\varphi\left({z}\right)\:=\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}\:\Rightarrow{Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:=\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)} \\ $$$$=\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)×\frac{\mathrm{4}\mid{ab}\mid}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\:=\frac{−{i}}{\mathrm{2}\mid{ab}\mid}\:\Rightarrow\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right)\:{dz}\:=\frac{\mathrm{2}{i}\pi×\left(−{i}\right)}{\mathrm{2}\mid{ab}\mid} \\ $$$$=\frac{\pi}{\mid{ab}\mid}\:\Rightarrow\:{I}\:=\frac{\pi}{\mid{a}\mid×\mid{b}\mid}\:\:\:\:\:\:\left({ab}\neq\mathrm{0}\right) \\ $$$${if}\:{a}={b}\:\neq\mathrm{0}\:\Rightarrow\:{I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{{a}^{\mathrm{2}} \:}\:=\frac{\pi}{{a}^{\mathrm{2}} } \\ $$
Commented by john santu last updated on 04/May/20
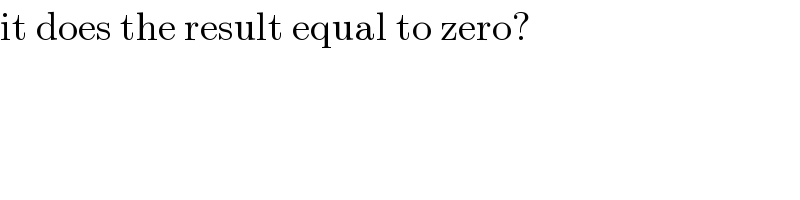
it does the result equal to zero?
$$\mathrm{it}\:\mathrm{does}\:\mathrm{the}\:\mathrm{result}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{zero}? \\ $$
Commented by john santu last updated on 04/May/20
waw via complex method
$$\mathrm{waw}\:\mathrm{via}\:\mathrm{complex}\:\mathrm{method} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *