0-pi-e-1-i-x-dx-

Question Number 51215 by gunawan last updated on 25/Dec/18

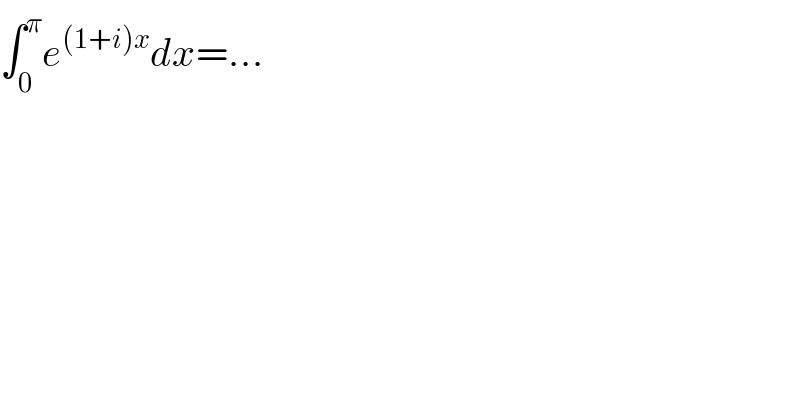
\int_{0}^{π} e^{(1 + i) x} d x = \dots

Answered by tanmay.chaudhury50@gmail.com last updated on 25/Dec/18

a = 1 + i

\int_{0}^{π} e^{a x} d x

= \frac{1}{a} ∣ e^{a x} ∣_{0}^{π}

= \frac{1}{a} (e^{a π} - 1)

= \frac{1}{1 + i} (e^{(1 + i) π} - 1)

= \frac{1 - i}{2} [e^{π} e^{i π} - 1] [e^{i π} = c o s π + i s i n π = - 1]

= \frac{1 - i}{2} (- e^{π} - 1)

= \frac{- 1 + i}{2} (e^{π} + 1)