Question Number 125050 by bramlexs22 last updated on 08/Dec/20
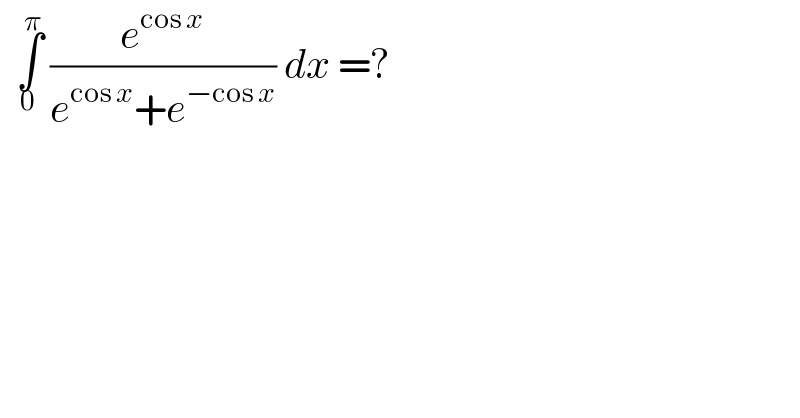
$$\:\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{e}^{\mathrm{cos}\:{x}} }{{e}^{\mathrm{cos}\:{x}} +{e}^{−\mathrm{cos}\:{x}} }\:{dx}\:=?\: \\ $$
Answered by liberty last updated on 08/Dec/20
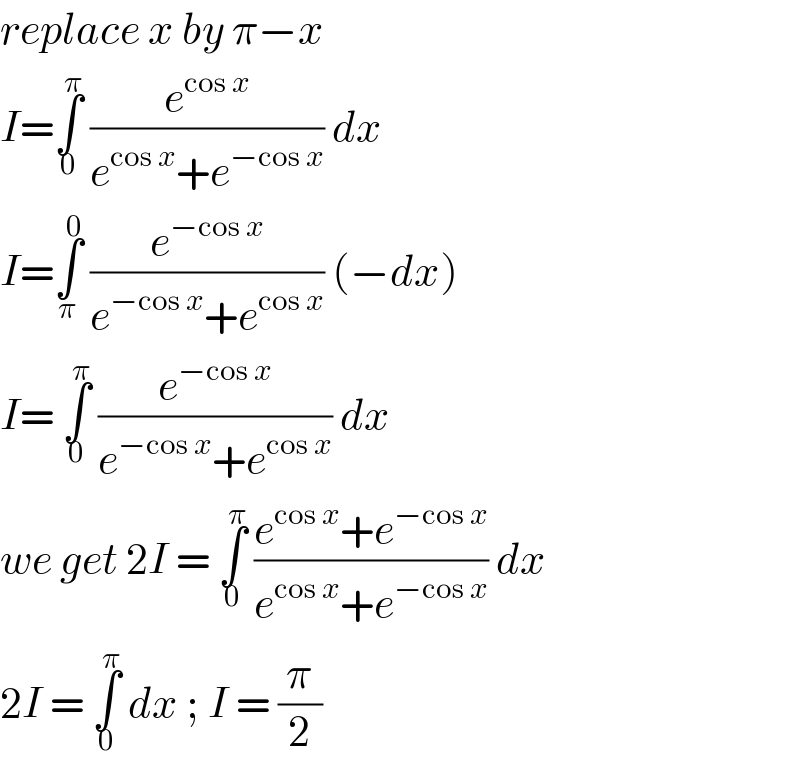
$${replace}\:{x}\:{by}\:\pi−{x}\: \\ $$$${I}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{e}^{\mathrm{cos}\:{x}} }{{e}^{\mathrm{cos}\:{x}} +{e}^{−\mathrm{cos}\:{x}} }\:{dx}\: \\ $$$${I}=\underset{\pi} {\overset{\mathrm{0}} {\int}}\:\frac{{e}^{−\mathrm{cos}\:{x}} }{{e}^{−\mathrm{cos}\:{x}} +{e}^{\mathrm{cos}\:{x}} }\:\left(−{dx}\right)\: \\ $$$${I}=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{e}^{−\mathrm{cos}\:{x}} }{{e}^{−\mathrm{cos}\:{x}} +{e}^{\mathrm{cos}\:{x}} }\:{dx}\: \\ $$$${we}\:{get}\:\mathrm{2}{I}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{e}^{\mathrm{cos}\:{x}} +{e}^{−\mathrm{cos}\:{x}} }{{e}^{\mathrm{cos}\:{x}} +{e}^{−\mathrm{cos}\:{x}} }\:{dx}\: \\ $$$$\mathrm{2}{I}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:{dx}\:;\:{I}\:=\:\frac{\pi}{\mathrm{2}} \\ $$
