Question Number 44232 by LYCON TRIX last updated on 24/Sep/18
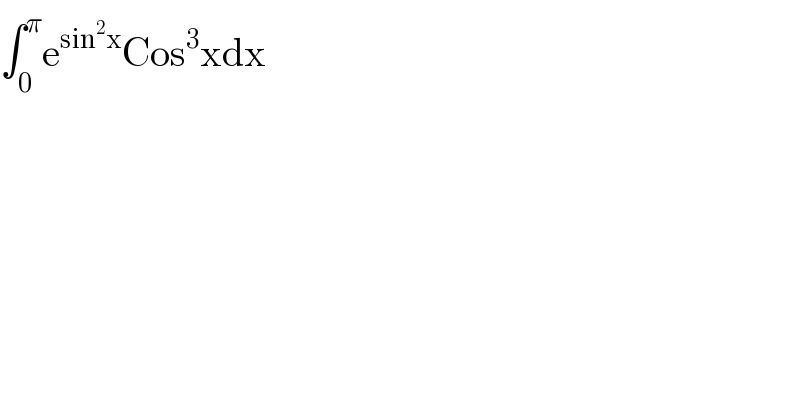
$$\int_{\mathrm{0}} ^{\pi} \mathrm{e}^{\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \mathrm{Cos}^{\mathrm{3}} \mathrm{xdx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Sep/18
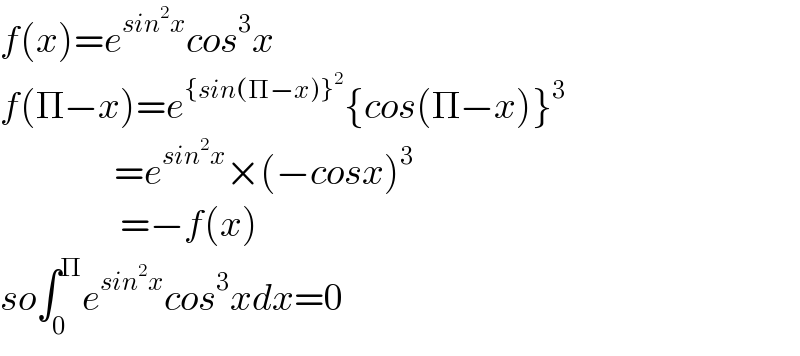
$${f}\left({x}\right)={e}^{{sin}^{\mathrm{2}} {x}} {cos}^{\mathrm{3}} {x} \\ $$$${f}\left(\Pi−{x}\right)={e}^{\left\{{sin}\left(\Pi−{x}\right)\right\}^{\mathrm{2}} } \left\{{cos}\left(\Pi−{x}\right)\right\}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={e}^{{sin}^{\mathrm{2}} {x}} ×\left(−{cosx}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−{f}\left({x}\right) \\ $$$${so}\int_{\mathrm{0}} ^{\Pi} {e}^{{sin}^{\mathrm{2}} {x}} {cos}^{\mathrm{3}} {xdx}=\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Sep/18
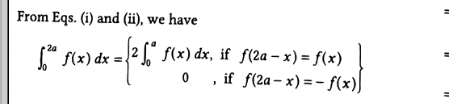
Commented by Hitarth Rana last updated on 24/Sep/18

$${Perfect}…\bigstar\bigstar\bigstar\bigstar\bigstar \\ $$
Commented by LYCON TRIX last updated on 24/Sep/18

$$\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{gentlemen} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Sep/18

$${thank}\:{you}… \\ $$
