Question Number 84810 by M±th+et£s last updated on 16/Mar/20
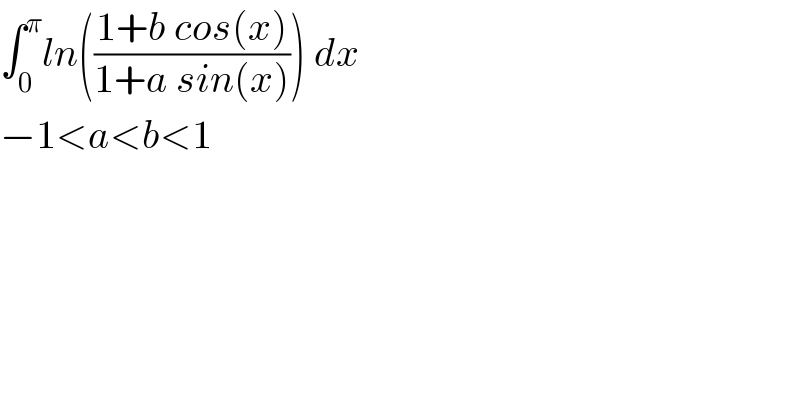
$$\int_{\mathrm{0}} ^{\pi} {ln}\left(\frac{\mathrm{1}+{b}\:{cos}\left({x}\right)}{\mathrm{1}+{a}\:{sin}\left({x}\right)}\right)\:{dx} \\ $$$$−\mathrm{1}<{a}<{b}<\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 16/Mar/20
![∫_0 ^π ln(((1+bcosx)/(1+asinx)))dx =g(b)−f(a) with g(b)=∫_0 ^π ln(1+bcosx)dx and f(a) =∫_0 ^π ln(1+asinx)dx we have g^′ (b)=∫_0 ^π ((cosx)/(1+bcosx))dx =(1/b)∫_0 ^π ((bcosx+1−1)/(1+bcosx))dx =(π/b)−(1/b)∫_0 ^π (dx/(1+bcosx)) ∫_0 ^π (dx/(1+bcosx)) =_(tan((x/2))=t) ∫_0 ^∞ (1/(1+b((1−t^2 )/(1+t^2 ))))×((2dt)/(1+t^2 )) =∫_0 ^∞ ((2dt)/(1+t^2 +b−bt^2 )) =∫_0 ^∞ ((2dt)/((1−b)t^2 +1+b)) =(2/(1−b))∫_0 ^∞ (dt/(t^2 +((1+b)/(1−b)))) =_(t=(√((1+b)/(1−b)))u) (2/(1−b))×((1−b)/(1+b))∫_0 ^∞ (1/(1+u^2 ))(√((1+b)/(1−b)))du =(2/( (√(1−b^2 ))))×(π/2) =(π/( (√(1−b^2 )))) ⇒g^′ (b)=(π/b)−(π/(b(√(1−b^2 )))) ⇒ g(b)=πln∣b∣−π ∫_b ^1 (dx/(x(√(1−x^2 )))) +K g(1) =K K=∫_0 ^π ln(1+cosx)dx ⇒g(b) =πln∣b∣−π ∫_b ^1 (dx/(x(√(1−x^2 )))) +∫_0 ^π ln(1+cosx)dx ∫_b ^1 (dx/(x(√(1−x^2 )))) =_(x=sinα) ∫_(arcsinb) ^(π/2) ((cosα dα)/(sinα.cosα)) =∫_(arcsinb) ^(π/2) (dα/(sinα)) =_(tan((α/2))=z) ∫_(tan(((arcsinb)/2))) ^1 ((2dz)/((1+z^2 )((2z)/(1+z^2 )))) =∫_(tan(((arcsinb)/2))) ^1 (dz/z) =[ln∣z∣]_(tan(((arcsinb)/2))) ^1 =−ln∣tan(((arcsinb)/2))) ⇒ g(b)=πln∣b∣+πln∣tan(((arcsinb)/2))∣+∫_0 ^π ln(1+cosx)dx ∫_0 ^π ln(1+cosx)dx =∫_0 ^π ln(2cos^2 ((x/2)))dx =πln(2)+2∫_0 ^π ln(cos((x/2)))dx ((x/2)=u) =πln(2)+2 ∫_0 ^(π/2) ln(cosu)(2du) =πln(2)+4(−(π/2)ln(2)) =−πln(2) ⇒ g(b)=π(ln∣b∣−ln(2))+πln∣tan(((arcsinb)/2))∣...be continued](https://www.tinkutara.com/question/Q84821.png)
$$\int_{\mathrm{0}} ^{\pi} {ln}\left(\frac{\mathrm{1}+{bcosx}}{\mathrm{1}+{asinx}}\right){dx}\:={g}\left({b}\right)−{f}\left({a}\right)\:{with}\:{g}\left({b}\right)=\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+{bcosx}\right){dx} \\ $$$${and}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+{asinx}\right){dx}\:\:{we}\:{have}\:{g}^{'} \left({b}\right)=\int_{\mathrm{0}} ^{\pi} \:\frac{{cosx}}{\mathrm{1}+{bcosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{{b}}\int_{\mathrm{0}} ^{\pi} \:\frac{{bcosx}+\mathrm{1}−\mathrm{1}}{\mathrm{1}+{bcosx}}{dx}\:=\frac{\pi}{{b}}−\frac{\mathrm{1}}{{b}}\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{\mathrm{1}+{bcosx}} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{\mathrm{1}+{bcosx}}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}+{b}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:+{b}−{bt}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}−{b}\right){t}^{\mathrm{2}} \:+\mathrm{1}+{b}}\:=\frac{\mathrm{2}}{\mathrm{1}−{b}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+{b}}{\mathrm{1}−{b}}} \\ $$$$=_{{t}=\sqrt{\frac{\mathrm{1}+{b}}{\mathrm{1}−{b}}}{u}} \:\:\frac{\mathrm{2}}{\mathrm{1}−{b}}×\frac{\mathrm{1}−{b}}{\mathrm{1}+{b}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\sqrt{\frac{\mathrm{1}+{b}}{\mathrm{1}−{b}}}{du} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }}\:\Rightarrow{g}^{'} \left({b}\right)=\frac{\pi}{{b}}−\frac{\pi}{{b}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${g}\left({b}\right)=\pi{ln}\mid{b}\mid−\pi\:\int_{{b}} ^{\mathrm{1}} \:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:+{K} \\ $$$${g}\left(\mathrm{1}\right)\:={K} \\ $$$${K}=\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+{cosx}\right){dx}\:\Rightarrow{g}\left({b}\right)\:=\pi{ln}\mid{b}\mid−\pi\:\int_{{b}} ^{\mathrm{1}} \:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:+\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+{cosx}\right){dx} \\ $$$$\int_{{b}} ^{\mathrm{1}} \:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=_{{x}={sin}\alpha} \:\:\:\int_{{arcsinb}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{cos}\alpha\:{d}\alpha}{{sin}\alpha.{cos}\alpha}\:=\int_{{arcsinb}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{d}\alpha}{{sin}\alpha} \\ $$$$=_{{tan}\left(\frac{\alpha}{\mathrm{2}}\right)={z}} \:\:\:\int_{{tan}\left(\frac{{arcsinb}}{\mathrm{2}}\right)} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dz}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\frac{\mathrm{2}{z}}{\mathrm{1}+{z}^{\mathrm{2}} }}\:=\int_{{tan}\left(\frac{{arcsinb}}{\mathrm{2}}\right)} ^{\mathrm{1}} \:\:\:\frac{{dz}}{{z}} \\ $$$$\left.=\left[{ln}\mid{z}\mid\right]_{{tan}\left(\frac{{arcsinb}}{\mathrm{2}}\right)} ^{\mathrm{1}} \:=−{ln}\mid{tan}\left(\frac{{arcsinb}}{\mathrm{2}}\right)\right)\:\Rightarrow \\ $$$${g}\left({b}\right)=\pi{ln}\mid{b}\mid+\pi{ln}\mid{tan}\left(\frac{{arcsinb}}{\mathrm{2}}\right)\mid+\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+{cosx}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+{cosx}\right){dx}\:=\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right){dx} \\ $$$$=\pi{ln}\left(\mathrm{2}\right)+\mathrm{2}\int_{\mathrm{0}} ^{\pi} \:{ln}\left({cos}\left(\frac{{x}}{\mathrm{2}}\right)\right){dx}\:\:\:\:\left(\frac{{x}}{\mathrm{2}}={u}\right) \\ $$$$=\pi{ln}\left(\mathrm{2}\right)+\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosu}\right)\left(\mathrm{2}{du}\right) \\ $$$$=\pi{ln}\left(\mathrm{2}\right)+\mathrm{4}\left(−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\right)\:=−\pi{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${g}\left({b}\right)=\pi\left({ln}\mid{b}\mid−{ln}\left(\mathrm{2}\right)\right)+\pi{ln}\mid{tan}\left(\frac{{arcsinb}}{\mathrm{2}}\right)\mid…{be}\:{continued} \\ $$
