Question Number 150103 by mnjuly1970 last updated on 09/Aug/21
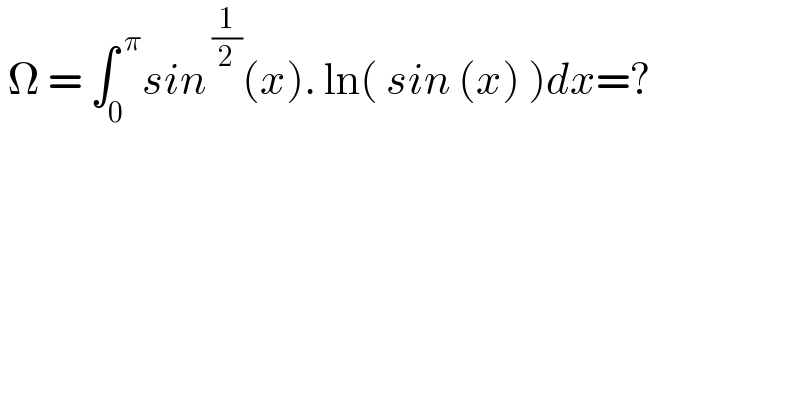
$$\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\pi} {sin}^{\:\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right).\:\mathrm{ln}\left(\:{sin}\:\left({x}\right)\:\right){dx}=? \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 09/Aug/21
![Ω=∫_0 ^π sin^(1/2) x∙ln(sinx)dx=2∫_0 ^(π/2) sin^(1/2) x∙ln(sinx)dx =2(∂/∂α)∣_(α=1) ∫_0 ^(π/2) sin^(α−(1/2)) (x)dx=2(∂/∂α)∣_(α=1) β((α/2)+(1/4),(1/2)) =2(∂/∂α)∣_(α=1) ((Γ((α/2)+(1/4))Γ((1/2)))/(Γ((α/2)+(3/4))))=2(√π)(∂/∂α)∣_(α=1) ((Γ((α/2)+(1/4)))/(Γ((α/2)+(3/4)))) =(√π)∣_(α=1) ((Γ((α/2)+(3/4))Γ′((α/2)+(1/4))−Γ((α/2)+(1/4))Γ′((α/2)+(3/4)))/(Γ^2 ((α/2)+(3/4)))) =(√π)[((Γ((5/4))Γ((3/4))(ψ((3/4))−ψ((5/4))))/(Γ^2 ((5/4))))] =4(√π)∙((Γ((3/4)))/(Γ((1/4))))(ψ((3/4))−ψ((1/4))−4) =((4π(√(2π)))/(Γ^2 ((1/4))))(π−4)=((4π(π−4)(√(2π)))/(Γ^2 ((1/4))))](https://www.tinkutara.com/question/Q150112.png)
$$\Omega=\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}\centerdot\mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}\centerdot\mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$$\:\:\:\:=\mathrm{2}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\alpha−\frac{\mathrm{1}}{\mathrm{2}}} \left({x}\right){dx}=\mathrm{2}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \beta\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:=\mathrm{2}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \frac{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)}=\mathrm{2}\sqrt{\pi}\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{1}} \frac{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$$\:\:\:\:=\sqrt{\pi}\mid_{\alpha=\mathrm{1}} \frac{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma'\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)−\Gamma\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma'\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)}{\Gamma^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$$\:\:\:\:=\sqrt{\pi}\left[\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\left(\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\right)}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{5}}{\mathrm{4}}\right)}\right] \\ $$$$\:\:\:\:=\mathrm{4}\sqrt{\pi}\centerdot\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}\left(\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{4}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{4}\pi\sqrt{\mathrm{2}\pi}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}\left(\pi−\mathrm{4}\right)=\frac{\mathrm{4}\pi\left(\pi−\mathrm{4}\right)\sqrt{\mathrm{2}\pi}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$ \\ $$
