Question Number 172741 by Kalebwizeman last updated on 30/Jun/22
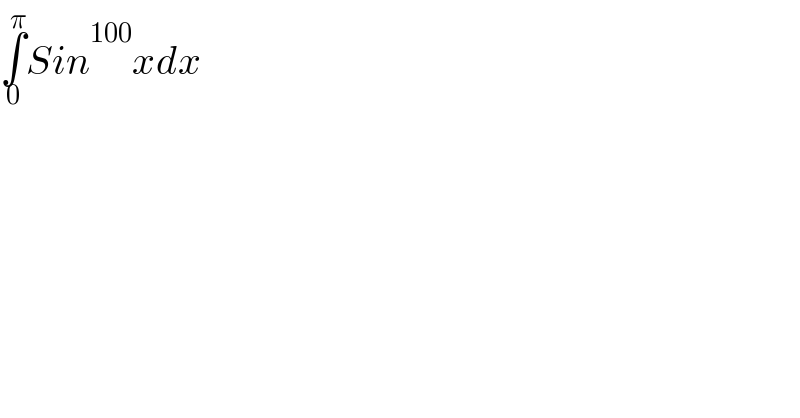
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}{Sin}\overset{\mathrm{100}} {\:}{xdx} \\ $$
Answered by aleks041103 last updated on 01/Jul/22
![I_n =2∫_0 ^(π/2) sin^n (x) dx sin^n x=(1−cos^2 x)sin^(n−2) x ⇒(1/2)I_n =∫_0 ^(π/2) sin^(n−2) x dx−∫_0 ^(π/2) cos^2 x sin^(n−2) x dx= =(1/2)I_(n−2) −∫_0 ^(π/2) (cosx)(cosx sin^(n−2) x dx)= =(1/2)I_(n−2) −∫_0 ^(π/2) (cosx)((sinx)^(n−2) d(sinx))= =(1/2)I_(n−2) −∫_0 ^(π/2) (cosx)d(((sin^(n−1) x)/(n−1)))= =(1/2)I_(n−2) −(1/(n−1))∫_0 ^(π/2) (cosx)d(sin^(n−1) x) ∫_0 ^(π/2) (cosx)d(sin^(n−1) x)= =[cosxsin^(n−1) x]_0 ^(π/2) −∫_0 ^(π/2) (sin^(n−1) x)d(cosx)= =∫_0 ^(π/2) sin^n x dx=(1/2)I_n ⇒I_n =I_(n−2) −(1/(n−1))I_n ⇒(1+(1/(n−1)))I_n =I_(n−2) ⇒I_n =((n−1)/n)I_(n−2) ⇒I_(2m) =((2m−1)/(2m))I_(2(m−1)) ⇒I_(2m) =(Π_(s=0) ^(k−1) ((2(m−s)−1)/(2(m−s))))I_(2(m−k)) k=m ⇒I_(2m) =(Π_(s=0) ^(m−1) ((2(m−s)−1)/(2(m−s))))I_0 I_0 =2∫_0 ^(π/2) sin^0 x dx=π ⇒I_(2m) =πΠ_(m−s=s′=1) ^m ((2s′−1)/(2s′)) I_(2m) =((1.3.5.7. ... .(2m−1))/(2.4.6.8. ... .(2m))) π ((1.3.5.7. ... .(2m−1))/(2.4.6.8. ... .(2m))) =((1.2.3. ... .(2m−1)(2m))/((2.4.6.8. ... .(2m))^2 ))=(((2m)!)/((2^m m!)^2 )) ⇒∫_0 ^π sin^(2m) x dx=(((2m)! π)/(4^m (m!)^2 )) ⇒∫_0 ^π sin^(100) x dx=((100!π)/(4^(100) (50!)^2 ))](https://www.tinkutara.com/question/Q172751.png)
$${I}_{{n}} =\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{{n}} \left({x}\right)\:{dx} \\ $$$${sin}^{{n}} {x}=\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){sin}^{{n}−\mathrm{2}} {x} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}{I}_{{n}} =\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{{n}−\mathrm{2}} {x}\:{dx}−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {cos}^{\mathrm{2}} {x}\:{sin}^{{n}−\mathrm{2}} {x}\:{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{I}_{{n}−\mathrm{2}} −\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cosx}\right)\left({cosx}\:{sin}^{{n}−\mathrm{2}} {x}\:{dx}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{I}_{{n}−\mathrm{2}} −\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cosx}\right)\left(\left({sinx}\right)^{{n}−\mathrm{2}} {d}\left({sinx}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{I}_{{n}−\mathrm{2}} −\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cosx}\right){d}\left(\frac{{sin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{I}_{{n}−\mathrm{2}} −\frac{\mathrm{1}}{{n}−\mathrm{1}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cosx}\right){d}\left({sin}^{{n}−\mathrm{1}} {x}\right) \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({cosx}\right){d}\left({sin}^{{n}−\mathrm{1}} {x}\right)= \\ $$$$=\left[{cosxsin}^{{n}−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} −\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({sin}^{{n}−\mathrm{1}} {x}\right){d}\left({cosx}\right)= \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{{n}} {x}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}{I}_{{n}} \\ $$$$\Rightarrow{I}_{{n}} ={I}_{{n}−\mathrm{2}} −\frac{\mathrm{1}}{{n}−\mathrm{1}}{I}_{{n}} \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{\mathrm{1}}{{n}−\mathrm{1}}\right){I}_{{n}} ={I}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{{n}−\mathrm{1}}{{n}}{I}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow{I}_{\mathrm{2}{m}} =\frac{\mathrm{2}{m}−\mathrm{1}}{\mathrm{2}{m}}{I}_{\mathrm{2}\left({m}−\mathrm{1}\right)} \\ $$$$\Rightarrow{I}_{\mathrm{2}{m}} =\left(\underset{{s}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\frac{\mathrm{2}\left({m}−{s}\right)−\mathrm{1}}{\mathrm{2}\left({m}−{s}\right)}\right){I}_{\mathrm{2}\left({m}−{k}\right)} \\ $$$${k}={m} \\ $$$$\Rightarrow{I}_{\mathrm{2}{m}} =\left(\underset{{s}=\mathrm{0}} {\overset{{m}−\mathrm{1}} {\prod}}\frac{\mathrm{2}\left({m}−{s}\right)−\mathrm{1}}{\mathrm{2}\left({m}−{s}\right)}\right){I}_{\mathrm{0}} \\ $$$${I}_{\mathrm{0}} =\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{\mathrm{0}} {x}\:{dx}=\pi \\ $$$$\Rightarrow{I}_{\mathrm{2}{m}} =\pi\underset{{m}−{s}={s}'=\mathrm{1}} {\overset{{m}} {\prod}}\frac{\mathrm{2}{s}'−\mathrm{1}}{\mathrm{2}{s}'} \\ $$$${I}_{\mathrm{2}{m}} =\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}.\:…\:.\left(\mathrm{2}{m}−\mathrm{1}\right)}{\mathrm{2}.\mathrm{4}.\mathrm{6}.\mathrm{8}.\:…\:.\left(\mathrm{2}{m}\right)}\:\pi \\ $$$$\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}.\:…\:.\left(\mathrm{2}{m}−\mathrm{1}\right)}{\mathrm{2}.\mathrm{4}.\mathrm{6}.\mathrm{8}.\:…\:.\left(\mathrm{2}{m}\right)}\:=\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}.\:…\:.\left(\mathrm{2}{m}−\mathrm{1}\right)\left(\mathrm{2}{m}\right)}{\left(\mathrm{2}.\mathrm{4}.\mathrm{6}.\mathrm{8}.\:…\:.\left(\mathrm{2}{m}\right)\right)^{\mathrm{2}} }=\frac{\left(\mathrm{2}{m}\right)!}{\left(\mathrm{2}^{{m}} {m}!\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} {sin}^{\mathrm{2}{m}} {x}\:{dx}=\frac{\left(\mathrm{2}{m}\right)!\:\pi}{\mathrm{4}^{{m}} \left({m}!\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi} {sin}^{\mathrm{100}} {x}\:{dx}=\frac{\mathrm{100}!\pi}{\mathrm{4}^{\mathrm{100}} \left(\mathrm{50}!\right)^{\mathrm{2}} } \\ $$
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Kalebwizeman last updated on 02/Jul/22
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
