Question Number 123896 by john_santu last updated on 29/Nov/20
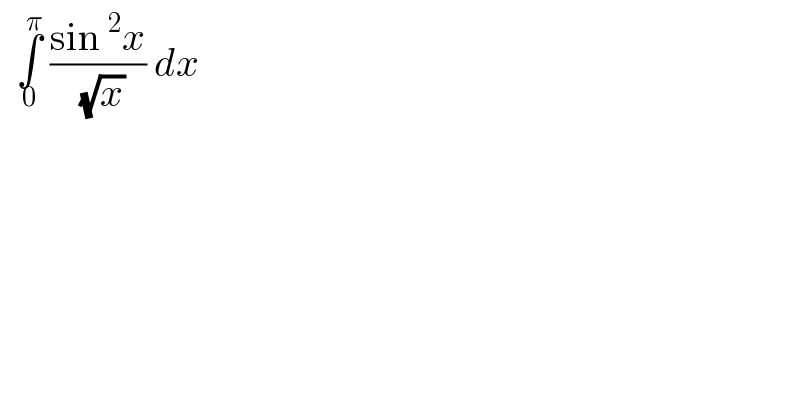
$$\:\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\:\sqrt{{x}}}\:{dx} \\ $$
Answered by mindispower last updated on 29/Nov/20
![sin^2 (x)=((1−cos(2x))/2) ⇔∫_0 ^π ((1−cos(2x))/(2(√x)))dx =∫_0 ^π (1/(2(√x)))−∫_0 ^π ((cos(2x))/( 2(√x)))dx=A−B x=((πt^2 )/4) =[(√x)]_0 ^π −∫_0 ^2 ((cos((π/2)t^2 ))/( (√π)t)).(π/2)tdt =(√π)−∫_0 ^2 ((cos(((πt^2 )/2)))/2)(√π)dt =(√π)−((√π)/2)∫_0 ^2 cos(π(t^2 /2))dt Recall ∫_0 ^u cos(π(t^2 /2))dt=C(u) Fernesl integral we get ∫_0 ^π ((sin^2 (t))/(2(√t)))dt=(√π)−((√π)/2)C(2)=((√π)/2)(2−C(2))](https://www.tinkutara.com/question/Q123901.png)
$${sin}^{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}\sqrt{{x}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}−\int_{\mathrm{0}} ^{\pi} \frac{{cos}\left(\mathrm{2}{x}\right)}{\:\mathrm{2}\sqrt{{x}}}{dx}={A}−{B} \\ $$$${x}=\frac{\pi{t}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\left[\sqrt{{x}}\right]_{\mathrm{0}} ^{\pi} −\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{cos}\left(\frac{\pi}{\mathrm{2}}{t}^{\mathrm{2}} \right)}{\:\sqrt{\pi}{t}}.\frac{\pi}{\mathrm{2}}{tdt} \\ $$$$=\sqrt{\pi}−\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{cos}\left(\frac{\pi{t}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{2}}\sqrt{\pi}{dt} \\ $$$$=\sqrt{\pi}−\frac{\sqrt{\pi}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} {cos}\left(\pi\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right){dt} \\ $$$${Recall}\:\int_{\mathrm{0}} ^{{u}} {cos}\left(\pi\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right){dt}={C}\left({u}\right)\:{Fernesl}\:{integral} \\ $$$${we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{sin}^{\mathrm{2}} \left({t}\right)}{\mathrm{2}\sqrt{{t}}}{dt}=\sqrt{\pi}−\frac{\sqrt{\pi}}{\mathrm{2}}{C}\left(\mathrm{2}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}\left(\mathrm{2}−{C}\left(\mathrm{2}\right)\right) \\ $$
