Question Number 91018 by M±th+et+s last updated on 27/Apr/20
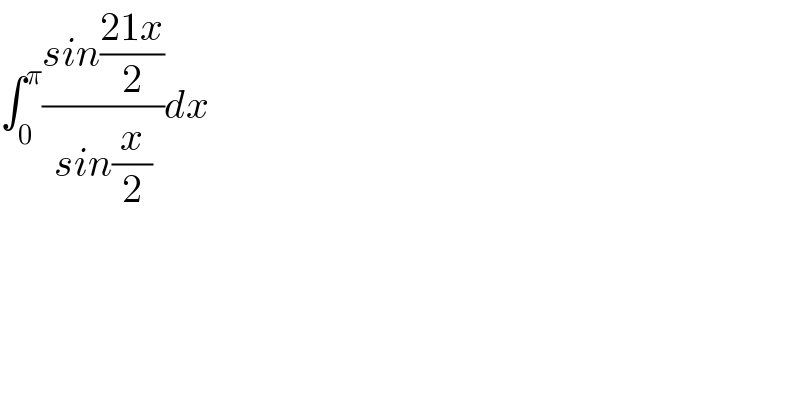
$$\int_{\mathrm{0}} ^{\pi} \frac{{sin}\frac{\mathrm{21}{x}}{\mathrm{2}}}{{sin}\frac{{x}}{\mathrm{2}}}{dx} \\ $$
Commented by mathmax by abdo last updated on 29/Apr/20
![let take atry changement (x/2) =t give ∫_0 ^π ((sin(((21x)/2)))/(sin((x/2))))dx =2∫_0 ^(π/2) ((sin(21t))/(sint))dt let w(t) =(1/(sint)) we have w(t) =(2/(e^(it) −e^(−it) )) =(2/(z−z^(−1) )) ( z=e^(it) ) =((2z)/(z^2 −1)) =−2z((1/(1−z^2 ))) =−2z Σ_(n=0) ^∞ z^(2n) =−2e^(it) Σ_(n=0) ^∞ e^(2int) ⇒ I =−4 ∫_0 ^(π/2) sin(21t)Σ_(n=0) ^∞ e^((2n+1)it) dt =−4 Σ_(n=0) ^∞ ∫_0 ^(π/2) sin(21t)e^((2n+1)t) dt =−4 Σ_(n=0) ^∞ A_n A_n =∫_0 ^(π/2) sin(21t)(cos(2n+1)t +isin(2n+1)t)dt =∫_0 ^(π/2) sin(21t)cos(2n+1)t +i ∫_0 ^(π/2) sin(21t)sin(2n+1)t dt sina cosb =cos((π/2)−a)cosb =(1/2)(cos((π/2)−a+b)+cos((π/2)−a−b)) =(1/2){sin(a−b)+sin(a+b)} ⇒ ∫_0 ^(π/2) sin(21t)cos(2n+1)t dt =(1/2)∫_0 ^(π/2) {sin(20−2n)t +sin(2n+22)t}dt =(1/2)[−(1/(20−2n))cos(20−2n)t+(1/(2n+22))cos(2n+22)t]_0 ^(π/2) =(1/2){−(1/(20−2n))cos(10−n)π+(1/(2n+22))cos(n+11)π +(1/(20−2n))−(1/(2n+22))}....be continued...](https://www.tinkutara.com/question/Q91260.png)
$${let}\:{take}\:{atry}\:\:{changement}\:\frac{{x}}{\mathrm{2}}\:={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\frac{{sin}\left(\frac{\mathrm{21}{x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\left(\mathrm{21}{t}\right)}{{sint}}{dt}\:\:{let}\:{w}\left({t}\right)\:=\frac{\mathrm{1}}{{sint}} \\ $$$${we}\:{have}\:{w}\left({t}\right)\:=\frac{\mathrm{2}}{{e}^{{it}} −{e}^{−{it}} }\:=\frac{\mathrm{2}}{{z}−{z}^{−\mathrm{1}} }\:\:\left(\:{z}={e}^{{it}} \right) \\ $$$$=\frac{\mathrm{2}{z}}{{z}^{\mathrm{2}} −\mathrm{1}}\:=−\mathrm{2}{z}\left(\frac{\mathrm{1}}{\mathrm{1}−{z}^{\mathrm{2}} }\right)\:=−\mathrm{2}{z}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{z}^{\mathrm{2}{n}} \:=−\mathrm{2}{e}^{{it}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{\mathrm{2}{int}} \:\Rightarrow \\ $$$${I}\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{21}{t}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:{e}^{\left(\mathrm{2}{n}+\mathrm{1}\right){it}} \:{dt} \\ $$$$=−\mathrm{4}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{21}{t}\right){e}^{\left(\mathrm{2}{n}+\mathrm{1}\right){t}} \:{dt}\:=−\mathrm{4}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{21}{t}\right)\left({cos}\left(\mathrm{2}{n}+\mathrm{1}\right){t}\:+{isin}\left(\mathrm{2}{n}+\mathrm{1}\right){t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{21}{t}\right){cos}\left(\mathrm{2}{n}+\mathrm{1}\right){t}\:+{i}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{21}{t}\right){sin}\left(\mathrm{2}{n}+\mathrm{1}\right){t}\:{dt} \\ $$$${sina}\:{cosb}\:={cos}\left(\frac{\pi}{\mathrm{2}}−{a}\right){cosb}\:=\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\left(\frac{\pi}{\mathrm{2}}−{a}+{b}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}−{a}−{b}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{sin}\left({a}−{b}\right)+{sin}\left({a}+{b}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{21}{t}\right){cos}\left(\mathrm{2}{n}+\mathrm{1}\right){t}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{{sin}\left(\mathrm{20}−\mathrm{2}{n}\right){t}\:+{sin}\left(\mathrm{2}{n}+\mathrm{22}\right){t}\right\}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{20}−\mathrm{2}{n}}{cos}\left(\mathrm{20}−\mathrm{2}{n}\right){t}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{22}}{cos}\left(\mathrm{2}{n}+\mathrm{22}\right){t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{\mathrm{1}}{\mathrm{20}−\mathrm{2}{n}}{cos}\left(\mathrm{10}−{n}\right)\pi+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{22}}{cos}\left({n}+\mathrm{11}\right)\pi\right. \\ $$$$\left.+\frac{\mathrm{1}}{\mathrm{20}−\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{22}}\right\}….{be}\:{continued}… \\ $$
