Question Number 167416 by Coronavirus last updated on 16/Mar/22
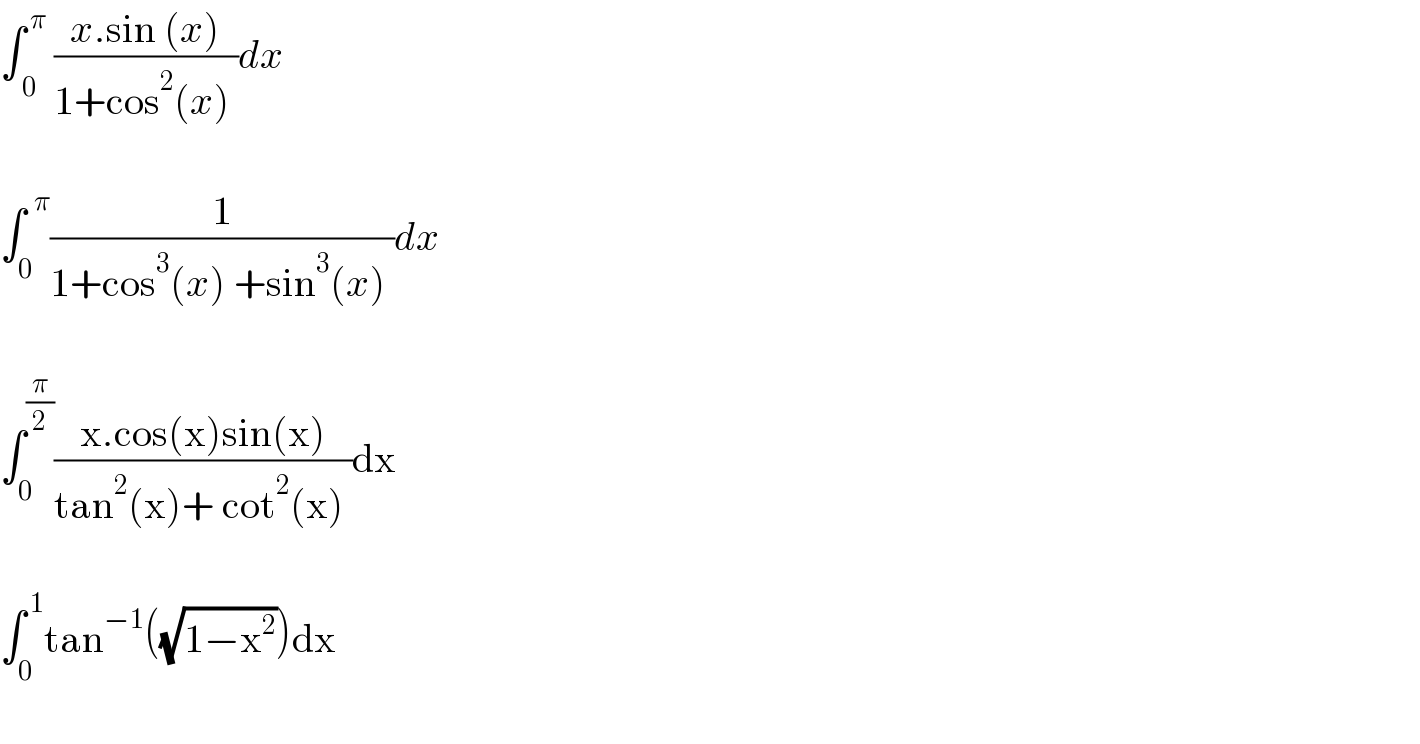
$$\int_{\:\mathrm{0}} ^{\:\pi} \:\frac{{x}.\mathrm{sin}\:\left({x}\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \left({x}\right)\:}{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\:\pi} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}^{\mathrm{3}} \left({x}\right)\:+\mathrm{sin}^{\mathrm{3}} \left({x}\right)\:}{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{x}.\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)+\:\mathrm{cot}^{\mathrm{2}} \left(\mathrm{x}\right)\:}\mathrm{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$ \\ $$
Commented by Coronavirus last updated on 16/Mar/22
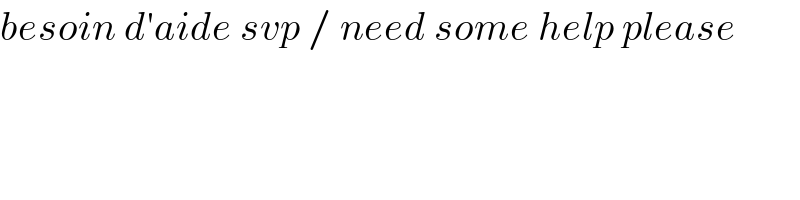
$${besoin}\:{d}'{aide}\:{svp}\:/\:{need}\:{some}\:{help}\:{please} \\ $$
Commented by Rasheed.Sindhi last updated on 17/Mar/22

$${hahahaha}… \\ $$
Commented by mr W last updated on 16/Mar/22

$${BioNTech},\:{Moderna},\:{Johnson}\:\&\:{Johnson} \\ $$$${etc}.\:{all}\:{may}\:{help}… \\ $$
