Question Number 55930 by ajfour last updated on 06/Mar/19
$$\int_{\mathrm{0}} ^{\:\:\pi} \frac{{x}\mathrm{tan}\:{x}}{\mathrm{sec}\:{x}+\mathrm{tan}\:{x}}{dx}\:=\:\left({is}\:{it}\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\pi\right)? \\ $$
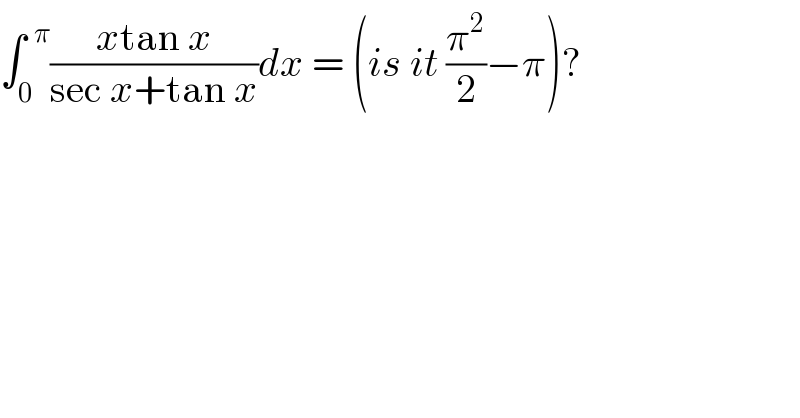
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19
$$\int_{\mathrm{0}} ^{\pi} \frac{{xsinx}}{\mathrm{1}+{sinx}}{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{x}\right){sin}\left(\pi−{x}\right)}{\mathrm{1}+{sin}\left(\pi−{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{x}\right){sinx}}{\mathrm{1}+{sinx}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi{sinx}−{xsinx}+{xsinx}}{\mathrm{1}+{sinx}}{dx} \\ $$$$\mathrm{2}{I}=\pi\int_{\mathrm{0}} ^{\pi} \frac{{sinx}}{\mathrm{1}+{sinx}}{dx} \\ $$$$=\pi\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{sinx}}\right){dx} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\int_{\mathrm{0}} ^{\pi} {dx}−\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}−{sinx}}{{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\int_{\mathrm{0}} ^{\pi} {dx}−\int_{\mathrm{0}} ^{\pi} {sec}^{\mathrm{2}} {xdx}+\int_{\mathrm{0}} ^{\pi} {secxtanxdx} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\mid{x}−{tanx}+{secx}\mid_{\mathrm{0}} ^{\pi} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\left(\pi−\mathrm{0}−\mathrm{1}\right)−\left(\mathrm{0}−\mathrm{0}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\pi−\mathrm{1}−\mathrm{1} \\ $$$$\mathrm{2}{I}=\pi^{\mathrm{2}} −\mathrm{2}\pi \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\pi \\ $$
Commented by ajfour last updated on 06/Mar/19
$${Thanks}\:{Sir},\:{great}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Mar/19
$${thank}\:{you}\:{sir}… \\ $$
Commented by maxmathsup by imad last updated on 09/Mar/19
![I =∫_0 ^π ((x(1+sinx−1))/(1+sinx))dx =∫_0 ^π xdx −∫_0 ^π (x/(1+sinx)) dx but ∫_0 ^π xdx =[(x^2 /2)]_0 ^π =(π^2 /2) and ∫_0 ^π (x/(1+sinx)) dx =_(tan((x/2))=t) ∫_0 ^∞ ((2arctan(t))/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =4 ∫_0 ^∞ ((arctan(t))/(1+t^2 +2t)) dt =4 ∫_0 ^∞ ((arctan(t))/((t+1)^2 )) dt ( and by parts) =4{ [−((arctan(t))/(t+1))]_0 ^∞ +∫_0 ^∞ (1/((t+1)(t^2 +1)))dt} =4 ∫_0 ^∞ (dt/((t+1)(t^2 +1))) dt let decompose F(t) =(1/((t+1)(t^2 +1))) ⇒ F(t) =(a/(t+1)) +((bt +c)/(t^2 +1)) a =lim_(t→−1) (t+1)F(t) = (1/2) lim_(t→+∞) tF(t) = 0 =a+b ⇒b =−a =−(1/2) ⇒F(t)=(1/(2(t+1))) +((−(t/2)+c)/(t^2 +1)) F(0) =1 =(1/2) +c ⇒c=(1/2) ⇒F(t)=(1/(2(t+1))) −(1/2) ((t−1)/(t^2 +1)) ⇒ ∫_0 ^∞ F(t)dt =(1/2)[ln∣t+1∣−(1/2)ln(t^2 +1)]_0 ^(+∞) +(1/2)[arctan(t)]_0 ^(+∞) =(1/2)[ln∣((t+1)/( (√(t^2 +1))))∣]_0 ^∞ +(π/4) =(π/4) ⇒ I =(π^2 /2) −4((π/4)) =(π^2 /2)−π .](https://www.tinkutara.com/question/Q56073.png)
$${I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{x}\left(\mathrm{1}+{sinx}−\mathrm{1}\right)}{\mathrm{1}+{sinx}}{dx}\:=\int_{\mathrm{0}} ^{\pi} \:{xdx}\:−\int_{\mathrm{0}} ^{\pi} \:\:\frac{{x}}{\mathrm{1}+{sinx}}\:{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:{xdx}\:=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\pi} =\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:\:\:{and}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{x}}{\mathrm{1}+{sinx}}\:{dx}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{arctan}\left({t}\right)}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}}\:{dt}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({t}\right)}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:\:\:\:\:\left(\:{and}\:{by}\:{parts}\right) \\ $$$$=\mathrm{4}\left\{\:\left[−\frac{{arctan}\left({t}\right)}{{t}+\mathrm{1}}\right]_{\mathrm{0}} ^{\infty} \:+\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}\right\} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{dt}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)\:=\:\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=−{a}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:+\frac{−\frac{{t}}{\mathrm{2}}+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+{c}\:\Rightarrow{c}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{F}\left({t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{t}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{+\infty} \:+\frac{\mathrm{1}}{\mathrm{2}}\left[{arctan}\left({t}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid\frac{{t}+\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} \:+\mathrm{1}}}\mid\right]_{\mathrm{0}} ^{\infty} \:+\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$${I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:−\mathrm{4}\left(\frac{\pi}{\mathrm{4}}\right)\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\pi\:\:. \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 06/Mar/19
![∫((xtan x)/(sec x +tan x))dx=∫((xsin x)/(1+sin x))dx=∫xdx−∫(x/(1+sin x))dx= =(x^2 /2)−∫(x/(1+sin x))dx= ∫(x/(1+sin x))dx= [∫u′v=uv−∫uv′; u′=(1/(1+sin x)); v=x u=−((cos x)/(1+sin x)); v′=1] =−((xcos x)/(1+sin x))+∫((cos x)/(1+sin x))dx= =−((xcos x)/(1+sin x))+ln (1+sin x) =(x^2 /2)+((xcos x)/(1+sin x))−ln (1+sin x) +C ⇒ your value is true](https://www.tinkutara.com/question/Q55938.png)
$$\int\frac{{x}\mathrm{tan}\:{x}}{\mathrm{sec}\:{x}\:+\mathrm{tan}\:{x}}{dx}=\int\frac{{x}\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}=\int{xdx}−\int\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}= \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\int\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}= \\ $$$$\:\:\:\:\:\int\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\int{u}'{v}={uv}−\int{uv}';\:{u}'=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}};\:{v}={x}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:{u}=−\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}};\:{v}'=\mathrm{1}\right] \\ $$$$\:\:\:\:\:=−\frac{{x}\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}+\int\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}= \\ $$$$\:\:\:\:\:=−\frac{{x}\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}+\mathrm{ln}\:\left(\mathrm{1}+\mathrm{sin}\:{x}\right) \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}−\mathrm{ln}\:\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\:+{C} \\ $$$$\Rightarrow\:\mathrm{your}\:\mathrm{value}\:\mathrm{is}\:\mathrm{true} \\ $$
Commented by ajfour last updated on 06/Mar/19
$${Thanks}\:{MJS}\:{Sir}! \\ $$