Question Number 182771 by liuxinnan last updated on 14/Dec/22
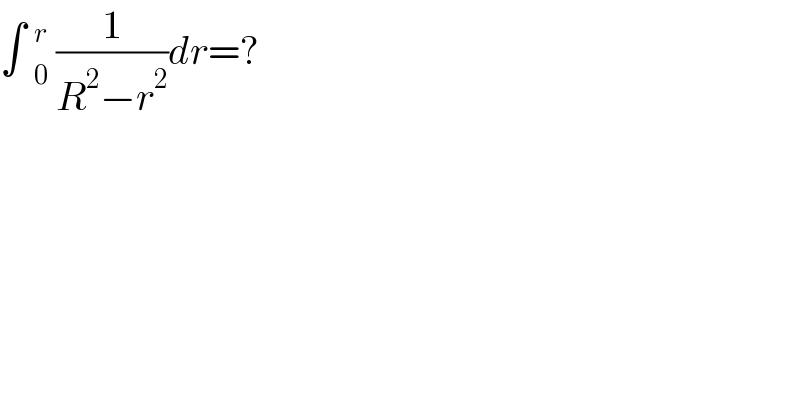
Commented by Frix last updated on 14/Dec/22

Commented by mr W last updated on 14/Dec/22
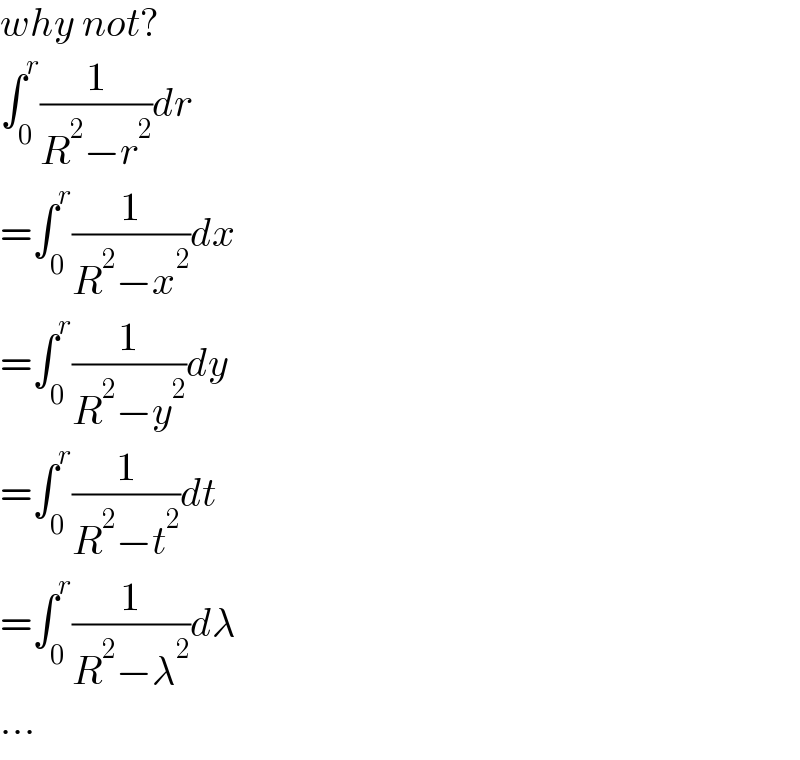
Commented by Frix last updated on 14/Dec/22
Commented by Frix last updated on 14/Dec/22

Commented by mr W last updated on 14/Dec/22
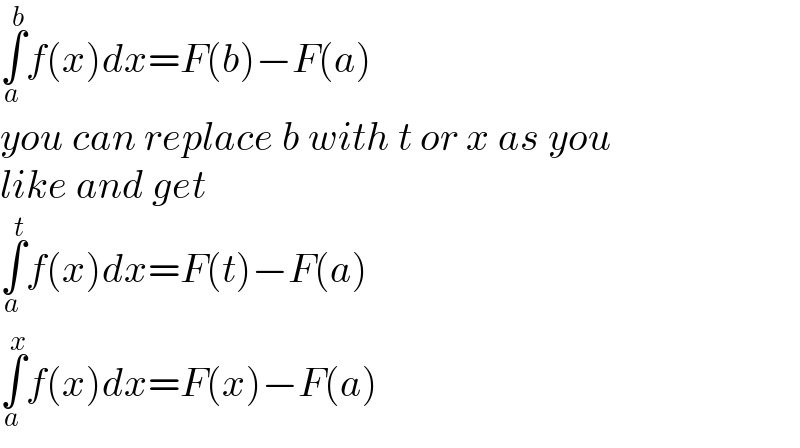
Commented by mr W last updated on 14/Dec/22
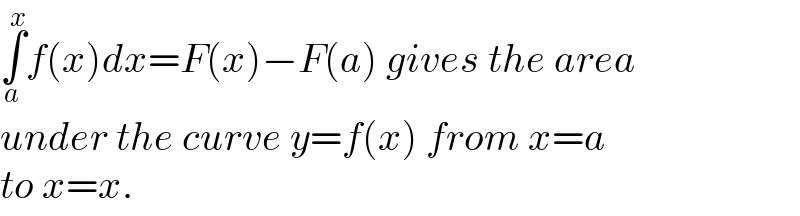
Commented by mr W last updated on 14/Dec/22
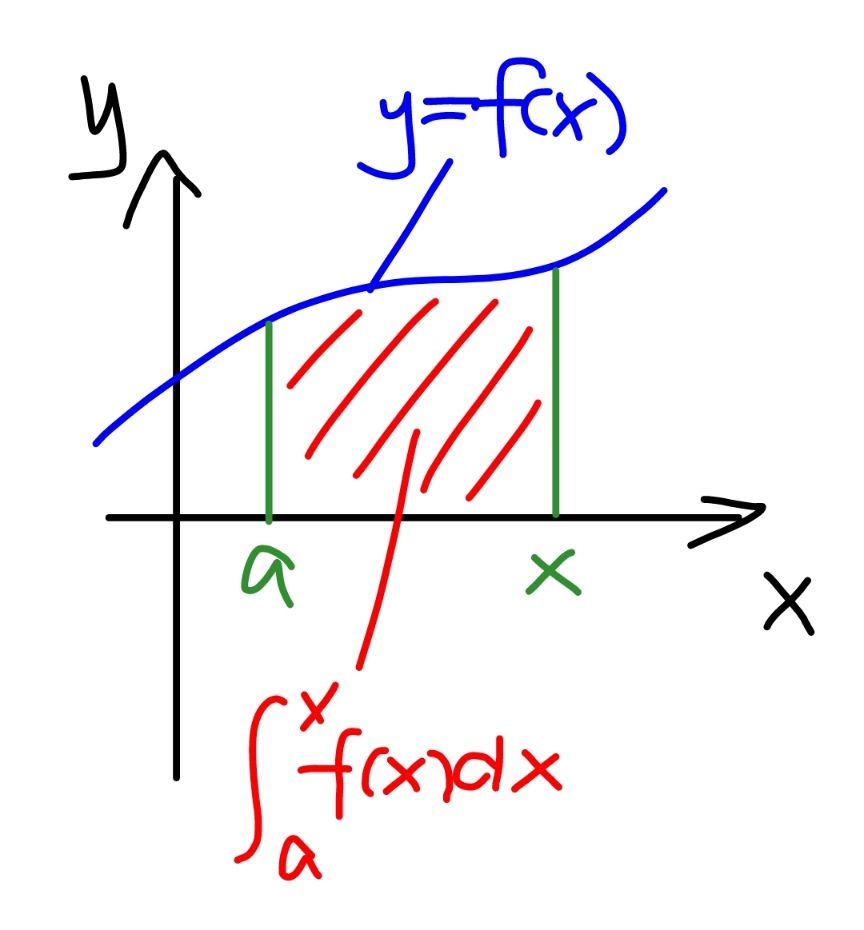
Answered by mr W last updated on 14/Dec/22
![∫_0 ^r (1/(R^2 −r^2 ))dr =(1/(2R))∫_0 ^r ((1/(R−r))+(1/(R+r)))dr =(1/(2R)) [ln ((R+r)/(R−r))]_0 ^r =(1/(2R)) ln ((R+r)/(R−r))](https://www.tinkutara.com/question/Q182778.png)
