Question Number 150828 by mnjuly1970 last updated on 15/Aug/21
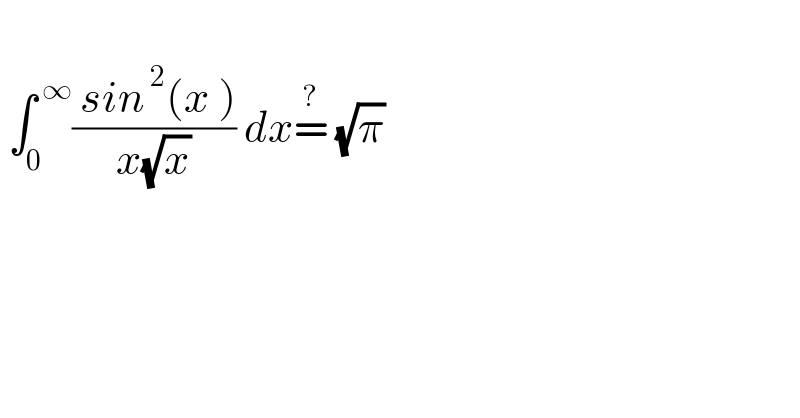
$$ \\ $$$$\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{sin}^{\:\mathrm{2}} \left({x}\:\right)}{{x}\sqrt{{x}}}\:{dx}\overset{?} {=}\:\sqrt{\pi} \\ $$
Answered by puissant last updated on 16/Aug/21
![Q=∫_0 ^∞ ((sin^2 x)/(x(√x)))dx =∫_0 ^∞ x^(−(3/2)) sin^2 xdx =[(1/(1−(3/2)))x^(−(1/2)) sin^2 x]_0 ^∞ −∫_0 ^∞ −2x^(−(1/2)) ×2sinxcosxdx =2∫_0 ^∞ ((sin2x)/( (√x)))dx =_( (√x)→u) 2∫_0 ^∞ ((sin2u^2 )/u)(2udu) =4∫_0 ^∞ sin2u^2 du = −4 im(∫_0 ^∞ e^(−2iu^2 ) du) ∵ ∵ ∵ ∫_0 ^∞ e^(−((√(2i))u)^2 ) du =_( (√(2i))u→z) ∫_0 ^z e^(−z^2 ) (dz/( (√(2i)))) =(1/( (√2)))e^(−i(π/4)) ×((√π)/2) =((√π)/(2(√2)))(((√2)/2)−i((√2)/2)) = ((√π)/4)−i((√π)/4) Q = −4 im(∫_0 ^∞ e^(−2iu^2 ) du) = −4(−((√π)/4)) ∵∴ Q = (√π).. ............Le puissant..........](https://www.tinkutara.com/question/Q150863.png)
$${Q}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}} {x}}{{x}\sqrt{{x}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {x}^{−\frac{\mathrm{3}}{\mathrm{2}}} {sin}^{\mathrm{2}} {xdx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}}{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} {sin}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} −\mathrm{2}{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\mathrm{2}{sinxcosxdx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\mathrm{2}{x}}{\:\sqrt{{x}}}{dx} \\ $$$$\underset{\:\sqrt{{x}}\rightarrow{u}} {=}\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\mathrm{2}{u}^{\mathrm{2}} }{{u}}\left(\mathrm{2}{udu}\right) \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {sin}\mathrm{2}{u}^{\mathrm{2}} {du}\:=\:−\mathrm{4}\:{im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{iu}^{\mathrm{2}} } {du}\right) \\ $$$$\:\because\:\:\:\because\:\:\:\because\:\:\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\sqrt{\mathrm{2}{i}}{u}\right)^{\mathrm{2}} } {du}\:\underset{\:\sqrt{\mathrm{2}{i}}{u}\rightarrow{z}} {=}\int_{\mathrm{0}} ^{{z}} {e}^{−{z}^{\mathrm{2}} } \frac{{dz}}{\:\sqrt{\mathrm{2}{i}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{e}^{−{i}\frac{\pi}{\mathrm{4}}} ×\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\:=\:\frac{\sqrt{\pi}}{\mathrm{4}}−{i}\frac{\sqrt{\pi}}{\mathrm{4}} \\ $$$${Q}\:=\:−\mathrm{4}\:{im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{iu}^{\mathrm{2}} } {du}\right)\:=\:−\mathrm{4}\left(−\frac{\sqrt{\pi}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\because\therefore\:\:{Q}\:=\:\sqrt{\pi}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:…………\mathscr{L}{e}\:{puissant}………. \\ $$
Commented by mnjuly1970 last updated on 16/Aug/21
$${thank}\:{you}\:{so}\:{much}… \\ $$
Answered by mathmax by abdo last updated on 17/Aug/21
![Υ=∫_0 ^∞ ((sin^2 (x))/(x(√x)))dx =_((√x)=t) ∫_0 ^∞ ((sin^2 (t^2 ))/t^3 )(2t)dt =2∫_0 ^∞ ((sin^2 (t^2 ))/t^2 )dt =2{ [−(1/t)sin^2 (t^2 )]_0 ^∞ −∫_0 ^∞ −(1/t)×2sin(t^2 )2t)cos(t^2 )dt} =2∫_0 ^∞ sin(2t^2 )dt =2∫_(−∞) ^(+∞) sin(2t^2 )dt =−2Im(∫_(−∞) ^(+∞) e^(−2it^2 ) dt) ∫_(−∞) ^(+∞) e^(−((√2)i)t^2 ) dt =_((√2)it=y) ∫_(−∞) ^(+∞) e^(−y^2 ) (dy/( (√2)i)) =((√π)/( (√2)e^((iπ)/4) ))=((√π)/( (√2)))e^(−((iπ)/4)) =((√π)/( (√2)))((1/( (√2)))−(i/( (√2))))=((√π)/2)−((i(√π))/2) ⇒ Υ=2×((√π)/2)=(√π)](https://www.tinkutara.com/question/Q150957.png)
$$\Upsilon=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}\sqrt{\mathrm{x}}}\mathrm{dx}\:=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}^{\mathrm{3}} }\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$\left.=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\mathrm{2}\left\{\:\:\left[−\frac{\mathrm{1}}{\mathrm{t}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{\mathrm{t}}×\mathrm{2sin}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{2t}\right)\mathrm{cos}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt}\right\} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\left(\mathrm{2t}^{\mathrm{2}} \right)\mathrm{dt}\:=\mathrm{2}\int_{−\infty} ^{+\infty} \:\mathrm{sin}\left(\mathrm{2t}^{\mathrm{2}} \right)\mathrm{dt}\:=−\mathrm{2Im}\left(\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{2it}^{\mathrm{2}} } \mathrm{dt}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\sqrt{\mathrm{2}}\mathrm{i}\right)\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=_{\sqrt{\mathrm{2}}\mathrm{it}=\mathrm{y}} \:\:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \frac{\mathrm{dy}}{\:\sqrt{\mathrm{2}}\mathrm{i}} \\ $$$$=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}−\frac{\mathrm{i}\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow \\ $$$$\Upsilon=\mathrm{2}×\frac{\sqrt{\pi}}{\mathrm{2}}=\sqrt{\pi} \\ $$
