Question Number 116500 by bobhans last updated on 04/Oct/20
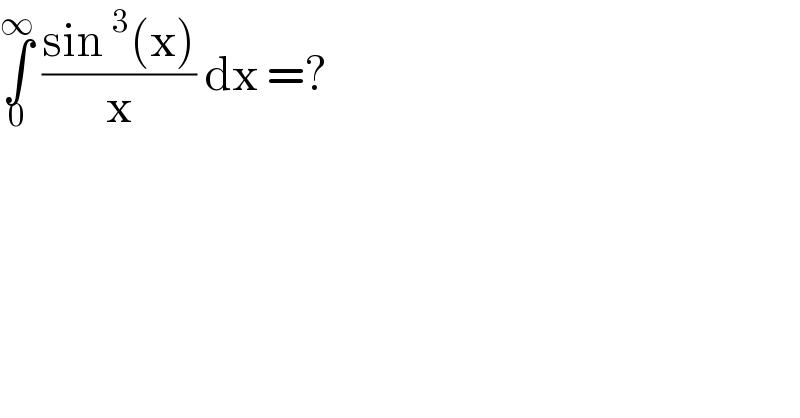
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{sin}\:^{\mathrm{3}} \left(\mathrm{x}\right)}{\mathrm{x}}\:\mathrm{dx}\:=? \\ $$
Answered by Olaf last updated on 04/Oct/20
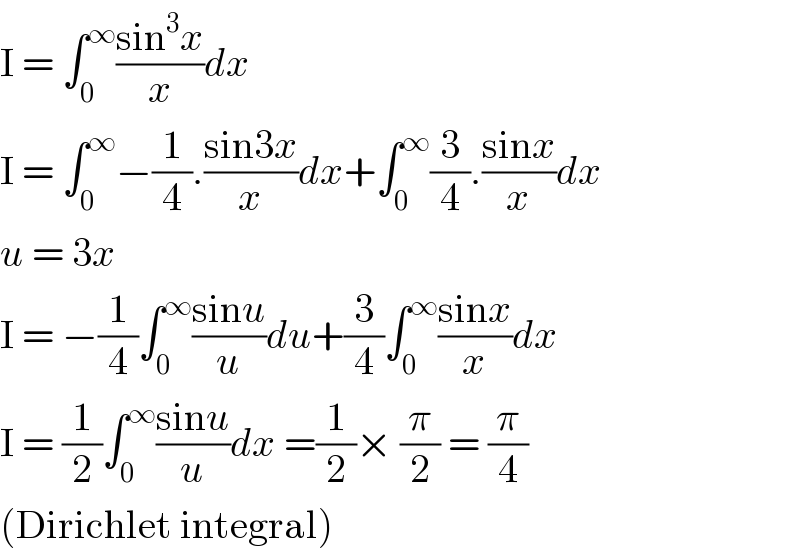
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} {x}}{{x}}{dx} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{sin3}{x}}{{x}}{dx}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{sin}{x}}{{x}}{dx} \\ $$$${u}\:=\:\mathrm{3}{x} \\ $$$$\mathrm{I}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{u}}{{u}}{du}+\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{x}}{{x}}{dx} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}{u}}{{u}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}×\:\frac{\pi}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\left(\mathrm{Dirichlet}\:\mathrm{integral}\right) \\ $$
Answered by Bird last updated on 04/Oct/20
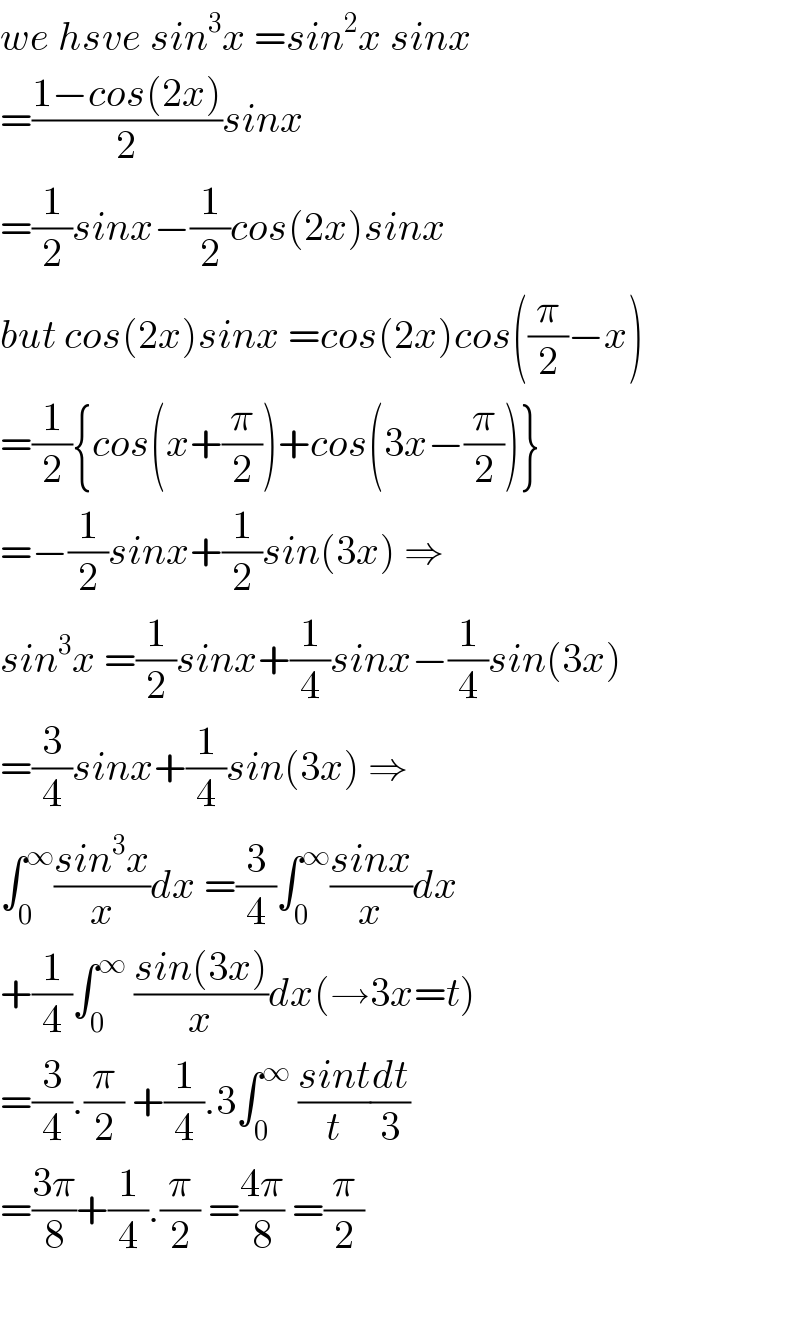
$${we}\:{hsve}\:{sin}^{\mathrm{3}} {x}\:={sin}^{\mathrm{2}} {x}\:{sinx} \\ $$$$=\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}{sinx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{sinx}−\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}{x}\right){sinx} \\ $$$${but}\:{cos}\left(\mathrm{2}{x}\right){sinx}\:={cos}\left(\mathrm{2}{x}\right){cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left({x}+\frac{\pi}{\mathrm{2}}\right)+{cos}\left(\mathrm{3}{x}−\frac{\pi}{\mathrm{2}}\right)\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{sinx}+\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{3}{x}\right)\:\Rightarrow \\ $$$${sin}^{\mathrm{3}} {x}\:=\frac{\mathrm{1}}{\mathrm{2}}{sinx}+\frac{\mathrm{1}}{\mathrm{4}}{sinx}−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{3}{x}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}{sinx}+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{3}{x}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{3}} {x}}{{x}}{dx}\:=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}}{dx} \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left(\mathrm{3}{x}\right)}{{x}}{dx}\left(\rightarrow\mathrm{3}{x}={t}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}.\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}.\mathrm{3}\int_{\mathrm{0}} ^{\infty} \:\frac{{sint}}{{t}}\frac{{dt}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\pi}{\mathrm{2}}\:=\frac{\mathrm{4}\pi}{\mathrm{8}}\:=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by Bird last updated on 04/Oct/20
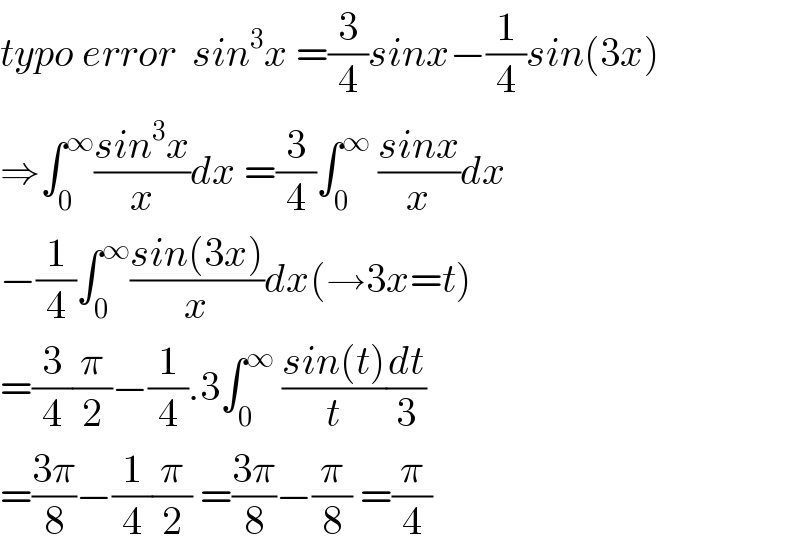
$${typo}\:{error}\:\:{sin}^{\mathrm{3}} {x}\:=\frac{\mathrm{3}}{\mathrm{4}}{sinx}−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{3}{x}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{3}} {x}}{{x}}{dx}\:=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}}{dx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\mathrm{3}{x}\right)}{{x}}{dx}\left(\rightarrow\mathrm{3}{x}={t}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}.\mathrm{3}\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left({t}\right)}{{t}}\frac{{dt}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}\frac{\pi}{\mathrm{2}}\:=\frac{\mathrm{3}\pi}{\mathrm{8}}−\frac{\pi}{\mathrm{8}}\:=\frac{\pi}{\mathrm{4}} \\ $$
