Question Number 128314 by 676597498 last updated on 06/Jan/21
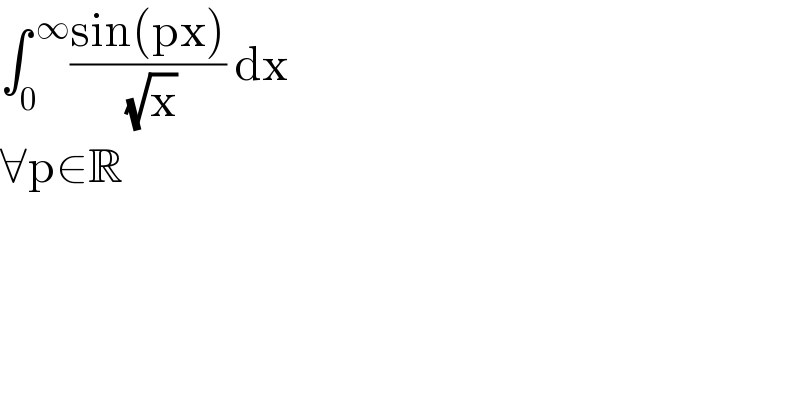
$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{sin}\left(\mathrm{px}\right)}{\:\sqrt{\mathrm{x}}}\:\mathrm{dx}\: \\ $$$$\forall\mathrm{p}\in\mathbb{R} \\ $$
Answered by Dwaipayan Shikari last updated on 06/Jan/21
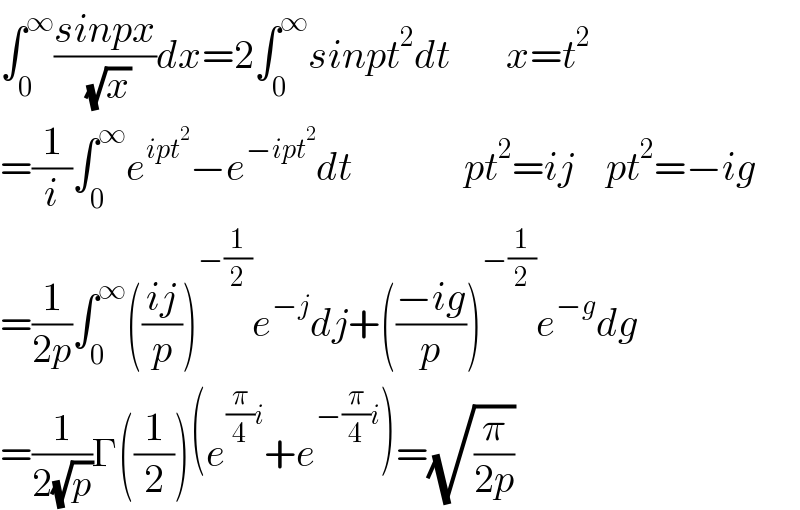
$$\int_{\mathrm{0}} ^{\infty} \frac{{sinpx}}{\:\sqrt{{x}}}{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {sinpt}^{\mathrm{2}} {dt}\:\:\:\:\:\:\:{x}={t}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{{i}}\int_{\mathrm{0}} ^{\infty} {e}^{{ipt}^{\mathrm{2}} } −{e}^{−{ipt}^{\mathrm{2}} } {dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{pt}^{\mathrm{2}} ={ij}\:\:\:\:{pt}^{\mathrm{2}} =−{ig} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{p}}\int_{\mathrm{0}} ^{\infty} \left(\frac{{ij}}{{p}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{j}} {dj}+\left(\frac{−{ig}}{{p}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{g}} {dg} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{p}}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left({e}^{\frac{\pi}{\mathrm{4}}{i}} +{e}^{−\frac{\pi}{\mathrm{4}}{i}} \right)=\sqrt{\frac{\pi}{\mathrm{2}{p}}} \\ $$
Answered by mnjuly1970 last updated on 06/Jan/21
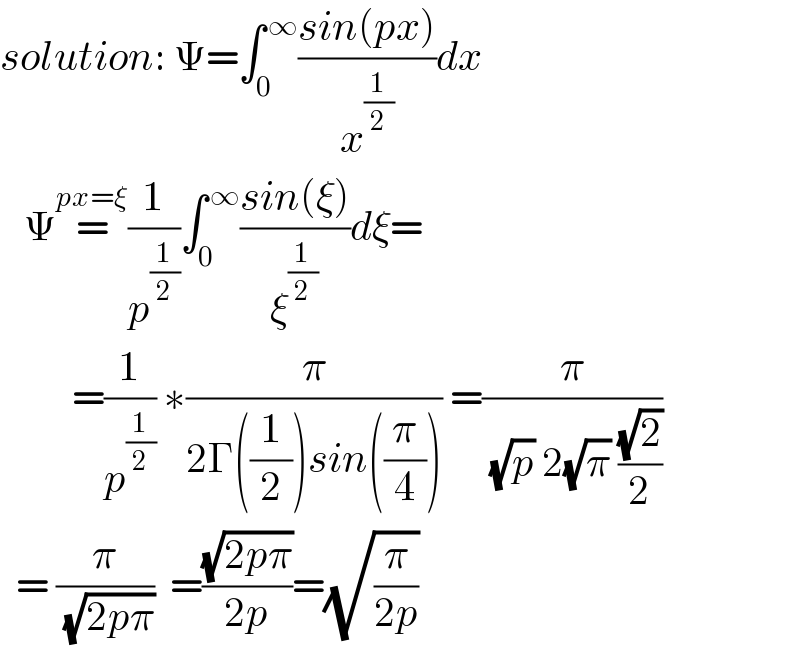
$${solution}:\:\Psi=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({px}\right)}{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{dx} \\ $$$$\:\:\:\Psi\overset{{px}=\xi} {=}\frac{\mathrm{1}}{{p}^{\frac{\mathrm{1}}{\mathrm{2}}} }\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left(\xi\right)}{\xi^{\frac{\mathrm{1}}{\mathrm{2}}} }{d}\xi= \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{p}^{\frac{\mathrm{1}}{\mathrm{2}}} }\:\ast\frac{\pi}{\mathrm{2}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right){sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\:\sqrt{{p}}\:\mathrm{2}\sqrt{\pi}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \\ $$$$\:\:=\:\frac{\pi}{\:\sqrt{\mathrm{2}{p}\pi}}\:\:=\frac{\sqrt{\mathrm{2}{p}\pi}}{\mathrm{2}{p}}=\sqrt{\frac{\pi}{\mathrm{2}{p}}} \\ $$
