Question Number 99228 by M±th+et+s last updated on 19/Jun/20
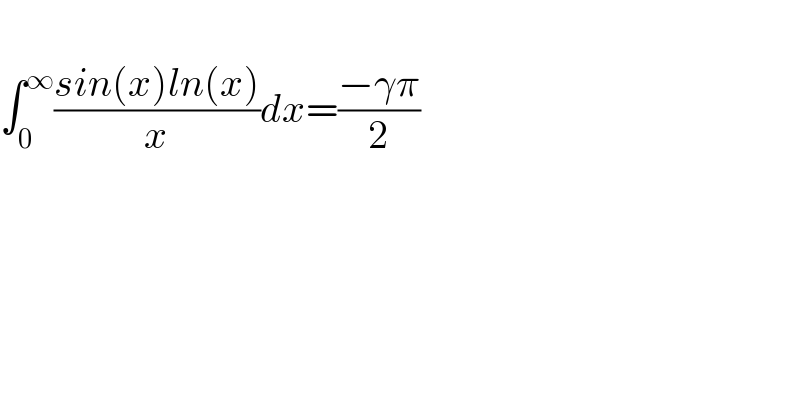
$$ \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right){ln}\left({x}\right)}{{x}}{dx}=\frac{−\gamma\pi}{\mathrm{2}} \\ $$
Answered by maths mind last updated on 20/Jun/20
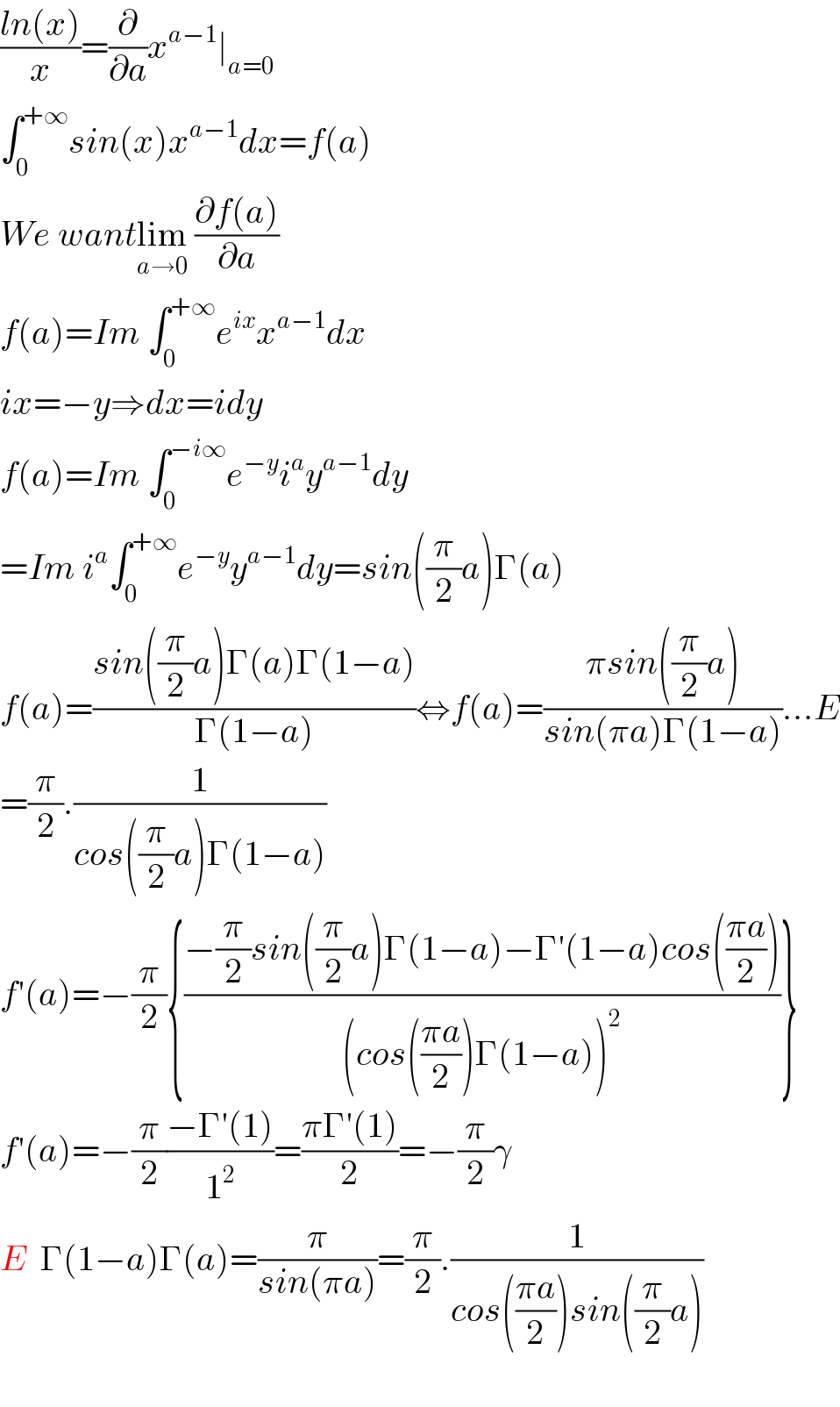
$$\frac{{ln}\left({x}\right)}{{x}}=\frac{\partial}{\partial{a}}{x}^{{a}−\mathrm{1}} \mid_{{a}=\mathrm{0}} \\ $$$$\int_{\mathrm{0}} ^{+\infty} {sin}\left({x}\right){x}^{{a}−\mathrm{1}} {dx}={f}\left({a}\right) \\ $$$${We}\:{want}\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\partial{f}\left({a}\right)}{\partial{a}} \\ $$$${f}\left({a}\right)={Im}\:\int_{\mathrm{0}} ^{+\infty} {e}^{{ix}} {x}^{{a}−\mathrm{1}} {dx} \\ $$$${ix}=−{y}\Rightarrow{dx}={idy} \\ $$$${f}\left({a}\right)={Im}\:\int_{\mathrm{0}} ^{−{i}\infty} {e}^{−{y}} {i}^{{a}} {y}^{{a}−\mathrm{1}} {dy} \\ $$$$={Im}\:{i}^{{a}} \int_{\mathrm{0}} ^{+\infty} {e}^{−{y}} {y}^{{a}−\mathrm{1}} {dy}={sin}\left(\frac{\pi}{\mathrm{2}}{a}\right)\Gamma\left({a}\right) \\ $$$${f}\left({a}\right)=\frac{{sin}\left(\frac{\pi}{\mathrm{2}}{a}\right)\Gamma\left({a}\right)\Gamma\left(\mathrm{1}−{a}\right)}{\Gamma\left(\mathrm{1}−{a}\right)}\Leftrightarrow{f}\left({a}\right)=\frac{\pi{sin}\left(\frac{\pi}{\mathrm{2}}{a}\right)}{{sin}\left(\pi{a}\right)\Gamma\left(\mathrm{1}−{a}\right)}…{E} \\ $$$$=\frac{\pi}{\mathrm{2}}.\frac{\mathrm{1}}{{cos}\left(\frac{\pi}{\mathrm{2}}{a}\right)\Gamma\left(\mathrm{1}−{a}\right)} \\ $$$${f}'\left({a}\right)=−\frac{\pi}{\mathrm{2}}\left\{\frac{−\frac{\pi}{\mathrm{2}}{sin}\left(\frac{\pi}{\mathrm{2}}{a}\right)\Gamma\left(\mathrm{1}−{a}\right)−\Gamma'\left(\mathrm{1}−{a}\right){cos}\left(\frac{\pi{a}}{\mathrm{2}}\right)}{\left({cos}\left(\frac{\pi{a}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−{a}\right)\right)^{\mathrm{2}} }\right\} \\ $$$${f}'\left({a}\right)=−\frac{\pi}{\mathrm{2}}\frac{−\Gamma'\left(\mathrm{1}\right)}{\mathrm{1}^{\mathrm{2}} }=\frac{\pi\Gamma'\left(\mathrm{1}\right)}{\mathrm{2}}=−\frac{\pi}{\mathrm{2}}\gamma \\ $$$${E}\:\:\Gamma\left(\mathrm{1}−{a}\right)\Gamma\left({a}\right)=\frac{\pi}{{sin}\left(\pi{a}\right)}=\frac{\pi}{\mathrm{2}}.\frac{\mathrm{1}}{{cos}\left(\frac{\pi{a}}{\mathrm{2}}\right){sin}\left(\frac{\pi}{\mathrm{2}}{a}\right)} \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 21/Jun/20

$${very}\:{good}\:{prof}.{math}\:{mind} \\ $$$${thank}\:{you} \\ $$
