Question Number 46502 by Ac Kesharwani last updated on 27/Oct/18
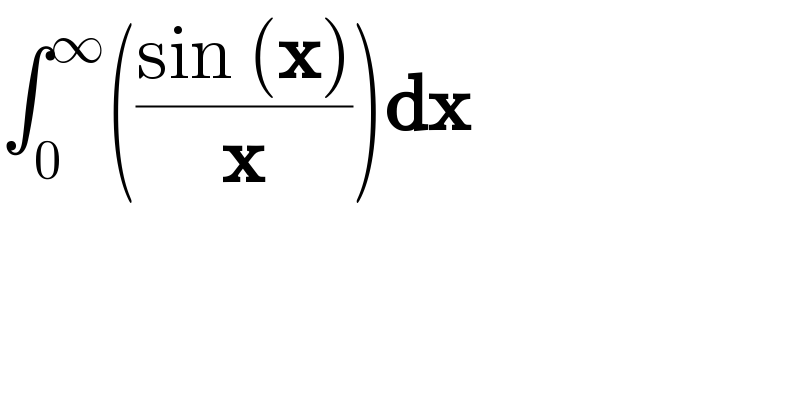
$$\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{sin}\:\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}}\right)\boldsymbol{\mathrm{dx}} \\ $$
Commented by math khazana by abdo last updated on 27/Oct/18
![let f(t)=∫_0 ^∞ ((sinx)/x)e^(−tx) dx with t≥0 we can prove that f is continue derivable on [0,+∞[ and we have f^′ (t)=−∫_0 ^∞ e^(−tx) sinx dx =−Im(∫_0 ^∞ e^(−tx+ix) dx) but ∫_0 ^∞ e^((−t+i)x) dx=[(1/(−t+i)) e^((−t+i)x) ]_(x=0) ^(+∞) =((−1)/(−t+i)) =(1/(t−i))=((t+i)/(t^2 +1)) ⇒f^′ (t)=−(1/(1+t^2 )) ⇒ f(t)=−arctan(t)+λ but ∃m>0 / ∣f(t)∣≤m∫_0 ^∞ e^(−tx) dx=(m/t)→0 (t→+∞)⇒λ=(π/2) f(t)=(π/2) −arctan(t) ⇒f(o)=∫_0 ^∞ ((sinx)/x)dx=(π/2) (arctan0=0)](https://www.tinkutara.com/question/Q46507.png)
$${let}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}}{e}^{−{tx}} {dx}\:{with}\:{t}\geqslant\mathrm{0}\:{we}\:{can}\:{prove}\: \\ $$$${that}\:{f}\:{is}\:{continue}\:{derivable}\:{on}\:\left[\mathrm{0},+\infty\left[\:{and}\:{we}\:{have}\right.\right. \\ $$$${f}^{'} \left({t}\right)=−\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}} {sinx}\:{dx}\:=−{Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}+{ix}} {dx}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{t}+{i}\right){x}} {dx}=\left[\frac{\mathrm{1}}{−{t}+{i}}\:{e}^{\left(−{t}+{i}\right){x}} \right]_{{x}=\mathrm{0}} ^{+\infty} =\frac{−\mathrm{1}}{−{t}+{i}} \\ $$$$=\frac{\mathrm{1}}{{t}−{i}}=\frac{{t}+{i}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow{f}^{'} \left({t}\right)=−\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}\left({t}\right)=−{arctan}\left({t}\right)+\lambda\:\:{but}\:\exists{m}>\mathrm{0}\:/ \\ $$$$\mid{f}\left({t}\right)\mid\leqslant{m}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tx}} {dx}=\frac{{m}}{{t}}\rightarrow\mathrm{0}\:\left({t}\rightarrow+\infty\right)\Rightarrow\lambda=\frac{\pi}{\mathrm{2}} \\ $$$${f}\left({t}\right)=\frac{\pi}{\mathrm{2}}\:−{arctan}\left({t}\right)\:\Rightarrow{f}\left({o}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}}{dx}=\frac{\pi}{\mathrm{2}} \\ $$$$\left({arctan}\mathrm{0}=\mathrm{0}\right) \\ $$
Answered by MJS last updated on 27/Oct/18
![∫((sin x)/x)dx=Si(x) [integral−sinus, table of values should exist somewhere in the www] Si(∞)−Si(0)=(π/2)](https://www.tinkutara.com/question/Q46506.png)
$$\int\frac{\mathrm{sin}\:{x}}{{x}}{dx}=\mathrm{Si}\left({x}\right)\:\left[\mathrm{integral}−\mathrm{sinus},\:\mathrm{table}\:\mathrm{of}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{values}\:\mathrm{should}\:\mathrm{exist}\:\mathrm{somewhere} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{in}\:\mathrm{the}\:\mathrm{www}\right] \\ $$$$\mathrm{Si}\left(\infty\right)−\mathrm{Si}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{2}} \\ $$
