Question Number 59882 by aliesam last updated on 15/May/19
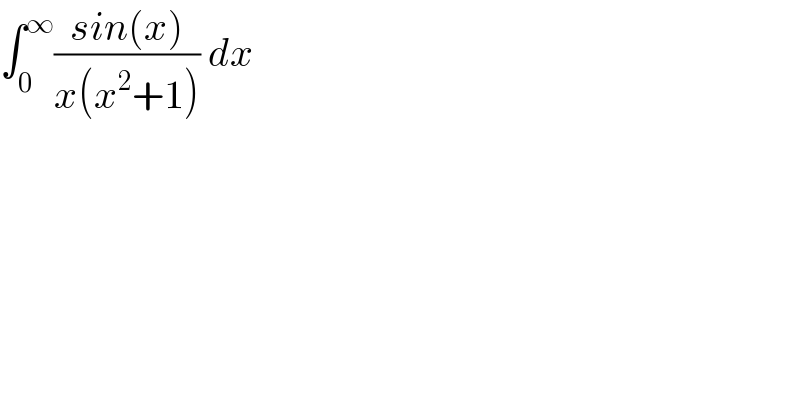
$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:{dx} \\ $$
Commented by maxmathsup by imad last updated on 15/May/19
$${you}\:{are}\:{welcome}. \\ $$
Commented by Mr X pcx last updated on 15/May/19
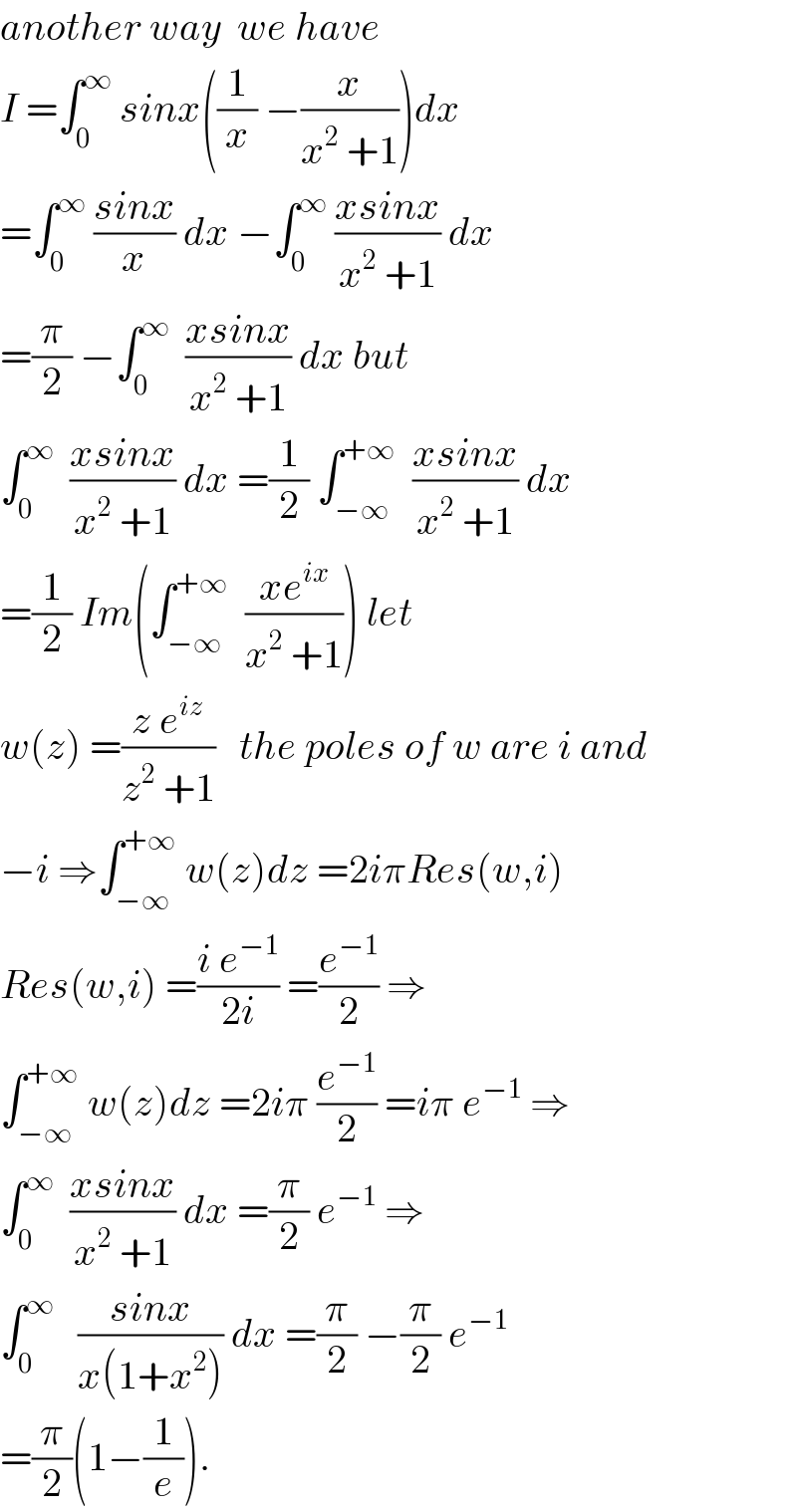
$${another}\:{way}\:\:{we}\:{have} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\infty} \:{sinx}\left(\frac{\mathrm{1}}{{x}}\:−\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}}\:{dx}\:−\int_{\mathrm{0}} ^{\infty} \:\frac{{xsinx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xsinx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xsinx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{xsinx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{Im}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{xe}^{{ix}} }{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\:{let}\: \\ $$$${w}\left({z}\right)\:=\frac{{z}\:{e}^{{iz}} }{{z}^{\mathrm{2}} \:+\mathrm{1}}\:\:\:{the}\:{poles}\:{of}\:{w}\:{are}\:{i}\:{and} \\ $$$$−{i}\:\Rightarrow\int_{−\infty} ^{+\infty} \:{w}\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left({w},{i}\right) \\ $$$${Res}\left({w},{i}\right)\:=\frac{{i}\:{e}^{−\mathrm{1}} }{\mathrm{2}{i}}\:=\frac{{e}^{−\mathrm{1}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{w}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{{e}^{−\mathrm{1}} }{\mathrm{2}}\:={i}\pi\:{e}^{−\mathrm{1}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xsinx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:=\frac{\pi}{\mathrm{2}}\:{e}^{−\mathrm{1}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{dx}\:=\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{2}}\:{e}^{−\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{e}}\right). \\ $$
Commented by aliesam last updated on 15/May/19

$${thank}\:{you}\:{sir}\: \\ $$
Commented by aliesam last updated on 15/May/19

$${thank}\:{you}\:{sir}\:{brilliant}\:{solution} \\ $$
Commented by malwaan last updated on 16/May/19
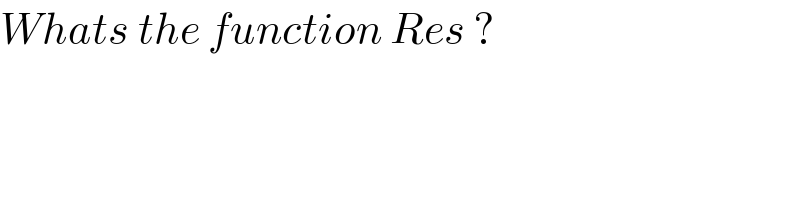
$${Whats}\:{the}\:{function}\:{Res}\:? \\ $$
