Question Number 146090 by Ar Brandon last updated on 10/Jul/21
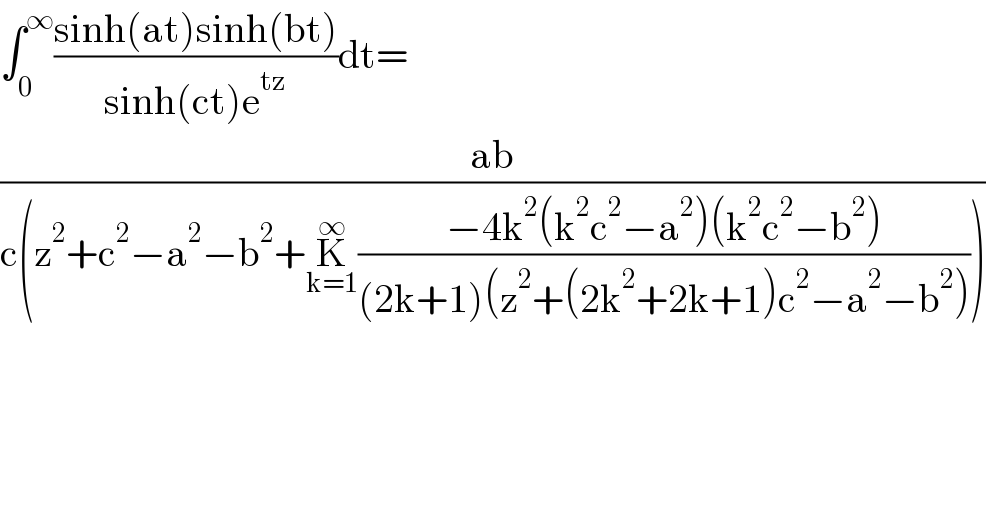
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sinh}\left(\mathrm{at}\right)\mathrm{sinh}\left(\mathrm{bt}\right)}{\mathrm{sinh}\left(\mathrm{ct}\right)\mathrm{e}^{\mathrm{tz}} }\mathrm{dt}= \\ $$$$\frac{\mathrm{ab}}{\mathrm{c}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} +\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\mathrm{K}}}\frac{−\mathrm{4k}^{\mathrm{2}} \left(\mathrm{k}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{k}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}{\left(\mathrm{2k}+\mathrm{1}\right)\left(\mathrm{z}^{\mathrm{2}} +\left(\mathrm{2k}^{\mathrm{2}} +\mathrm{2k}+\mathrm{1}\right)\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)}\right)} \\ $$
Answered by mindispower last updated on 10/Jul/21

$${z}\:{is}\:{x}\:? \\ $$
Commented by Ar Brandon last updated on 10/Jul/21

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{remark}.\:\mathrm{I}\:\mathrm{appologize}\:\mathrm{for}\:\mathrm{that}. \\ $$$$\mathrm{It}\:\mathrm{was}\:\mathrm{a}\:\mathrm{mistake},\:\mathrm{it}'\mathrm{s}\:\mathrm{been}\:\mathrm{edited}. \\ $$
Answered by mindispower last updated on 14/Jul/21

$${tchek}\:{it}\:{sir} \\ $$
