Menu Close

0-sinx-2-1-x-4-dx-0-4009-prove-that-

Tinku Tara 0 Comments
Pin




Question Number 85999 by M±th+et£s last updated on 26/Mar/20
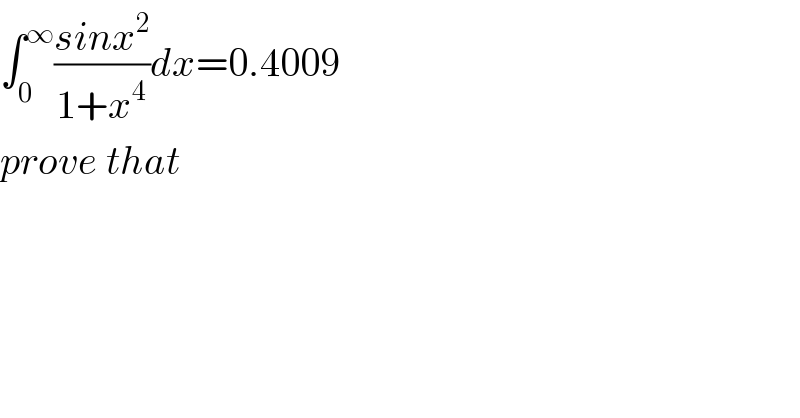
∫_0 ^∞ ((sinx^2 )/(1+x^4 ))dx=0.4009 prove that
$$\int_{\mathrm{0}} ^{\infty} \frac{{sinx}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx}=\mathrm{0}.\mathrm{4009} \\ $$$${prove}\:{that} \\ $$
Commented by MJS last updated on 26/Mar/20
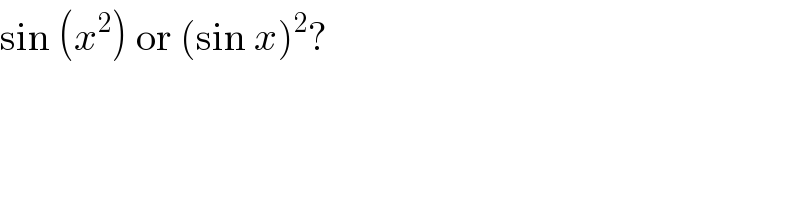
sin (x^2 ) or (sin x)^2 ?
$$\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)\:\mathrm{or}\:\left(\mathrm{sin}\:{x}\right)^{\mathrm{2}} ? \\ $$
Commented by john santu last updated on 26/Mar/20
may be sin (x^2 )
$${may}\:{be}\:\mathrm{sin}\:\left({x}^{\mathrm{2}} \right) \\ $$
Commented by M±th+et£s last updated on 26/Mar/20
sin(x^2 )
$${sin}\left({x}^{\mathrm{2}} \right)\: \\ $$
Commented by mathmax by abdo last updated on 26/Mar/20
I=∫_0 ^∞ ((sin(x^2 ))/(x^4 +1))dx ⇒2I = ∫_(−∞) ^(+∞) ((sin(x^2 ))/(x^4 +1))dx =Im(∫_(−∞) ^(+∞) (e^(ix^2 ) /(x^4 +1))dx) letϕ(z)=(e^(iz^2 ) /(z^4 +1)) ⇒ϕ(z) =(e^(iz^2 ) /((z^2 −i)(z^2 +i))) =(e^(iz^2 ) /((z−(√i))(z+(√i))(z−(√(−i)))(z+(√(−i))))) =(e^(iz^2 ) /((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{Res(ϕ,e^((iπ)/4) )+Res(ϕ,−e^(−((iπ)/4)) )} Res(ϕ,e^((iπ)/4) ) =(e^(ie^((iπ)/2) ) /(2e^((iπ)/4) (2i))) =((e^(−1) e^(−((iπ)/4)) )/(4i)) Res(ϕ,−e^(−((iπ)/4)) ) = (e^(i(−i)) /(−2e^(−((iπ)/4)) (−2i))) =((e e^((iπ)/4) )/(4i)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (e^(−1) /(4i))e^(−((iπ)/4)) +(e/(4i))e^((iπ)/4) } =(π/2){ e^(−1) ((1/( (√2)))−(i/( (√2)))) +e((1/( (√2))) +(i/( (√2))))} =(π/2){ ((e+e^(−1) )/( (√2))) +i(((e−e^(−1) )/( (√2))))} ⇒2I =(π/(2(√2)))(e−e^(−1) ) ⇒ I =(π/(4(√2)))(e−e^(−1) )
$${I}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{4}} +\mathrm{1}}{dx}\:\Rightarrow\mathrm{2}{I}\:=\:\int_{−\infty} ^{+\infty} \:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{4}} \:+\mathrm{1}}{dx}\:={Im}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{ix}^{\mathrm{2}} } }{{x}^{\mathrm{4}} \:+\mathrm{1}}{dx}\right) \\ $$$${let}\varphi\left({z}\right)=\frac{{e}^{{iz}^{\mathrm{2}} } }{{z}^{\mathrm{4}} \:+\mathrm{1}}\:\Rightarrow\varphi\left({z}\right)\:=\frac{{e}^{{iz}^{\mathrm{2}} } }{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)} \\ $$$$=\frac{{e}^{{iz}^{\mathrm{2}} } }{\left({z}−\sqrt{{i}}\right)\left({z}+\sqrt{{i}}\right)\left({z}−\sqrt{−{i}}\right)\left({z}+\sqrt{−{i}}\right)}\:=\frac{{e}^{{iz}^{\mathrm{2}} } }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$${residus}\:{theorem}\:{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{{e}^{{ie}^{\frac{{i}\pi}{\mathrm{2}}} } }{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)}\:=\frac{{e}^{−\mathrm{1}} \:{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}{i}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:=\:\frac{{e}^{{i}\left(−{i}\right)} }{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \left(−\mathrm{2}{i}\right)}\:=\frac{{e}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\:\frac{{e}^{−\mathrm{1}} }{\mathrm{4}{i}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:+\frac{{e}}{\mathrm{4}{i}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\left\{\:\:{e}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\:+{e}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\left\{\:\frac{{e}+{e}^{−\mathrm{1}} }{\:\sqrt{\mathrm{2}}}\:+{i}\left(\frac{{e}−{e}^{−\mathrm{1}} }{\:\sqrt{\mathrm{2}}}\right)\right\}\:\Rightarrow\mathrm{2}{I}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\left({e}−{e}^{−\mathrm{1}} \right)\:\Rightarrow \\ $$$${I}\:=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\left({e}−{e}^{−\mathrm{1}} \right) \\ $$
Commented by mind is power last updated on 27/Mar/20
Sir for θ∈[(π/2),π] C=Re^(iθ) (e^(iz^2 ) /(1+z^4 ))=(e^(iR^2 (cos(2θ)+isin(2θ))) /(1+R^4 e^(4iθ) ))=(e^(−R^2 sin(2θ)) /(1+R^4 e^(4iθ) )) ,sin(2θ)<0 lim_(R→∞) ∫_C (e^(iz^2 ) /(1+z^4 ))dz #0
$${Sir}\:\:\:{for}\:\theta\in\left[\frac{\pi}{\mathrm{2}},\pi\right]\:\:\:{C}={Re}^{{i}\theta} \\ $$$$\frac{{e}^{{iz}^{\mathrm{2}} } }{\mathrm{1}+{z}^{\mathrm{4}} }=\frac{{e}^{{iR}^{\mathrm{2}} \left({cos}\left(\mathrm{2}\theta\right)+{isin}\left(\mathrm{2}\theta\right)\right)} }{\mathrm{1}+{R}^{\mathrm{4}} {e}^{\mathrm{4}{i}\theta} }=\frac{{e}^{−{R}^{\mathrm{2}} {sin}\left(\mathrm{2}\theta\right)} }{\mathrm{1}+{R}^{\mathrm{4}} {e}^{\mathrm{4}{i}\theta} }\:\:,{sin}\left(\mathrm{2}\theta\right)<\mathrm{0} \\ $$$$\underset{{R}\rightarrow\infty} {\mathrm{lim}}\int_{{C}} \frac{{e}^{{iz}^{\mathrm{2}} } }{\mathrm{1}+{z}^{\mathrm{4}} }{dz}\:\:#\mathrm{0} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *