Question Number 168743 by mehdiAz last updated on 16/Apr/22
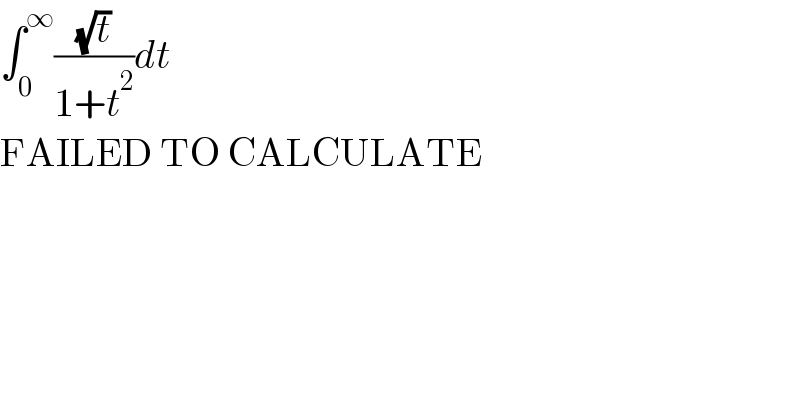
$$\int_{\mathrm{0}} ^{\infty} \frac{\sqrt{{t}}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\mathrm{FAILED}\:\mathrm{TO}\:\mathrm{CALCULATE} \\ $$$$ \\ $$
Commented by GalaxyBills last updated on 17/Apr/22

$$\int_{\mathrm{0}} ^{\infty} \frac{\sqrt{{t}}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\mathrm{FAILED}\:\mathrm{TO}\:\mathrm{CALCULATE} \\ $$$$\mathfrak{S}{olution}\:\:{by}\:{Awudulai} \\ $$🇬🇭
$${let}\:{t}={u}^{\mathrm{2}} \rightarrow{dt}=\mathrm{2}{udu} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{u}\sqrt{{u}^{\mathrm{2}} }}{\mathrm{1}+{u}^{\mathrm{4}} }{du}\rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{4}} }{du} \\ $$$${let}\:{z}={u}^{\mathrm{4}} \overset{{u}={z}^{\frac{\mathrm{1}}{\mathrm{4}}} } {\rightarrow}{dz}=\mathrm{4}{u}^{\mathrm{3}} \Rightarrow{du}=\frac{{dz}}{\mathrm{4}{u}^{\mathrm{3}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{u}^{\mathrm{2}} .{u}^{−\mathrm{3}} }{\mathrm{4}\left(\mathrm{1}+{z}\right)}{dz}\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{z}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{1}+{z}\right)}{dz} \\ $$$${using}\:\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{m}−\mathrm{1}} }{\left(\mathrm{1}+{x}\right)^{{m}+{n}} }{dx}\rightarrow\Gamma\left({m}\right)\Gamma\left({n}\right) \\ $$$${m}=\frac{\mathrm{3}}{\mathrm{4}}\:\:{amd}\:{n}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\right)=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{2}\pi}{\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$Kudos to my Mentors: Prempeh (Euclid)🇬🇭 and to Daniel (Small Einstein)🇳🇬
$${let}\:{t}={u}^{\mathrm{2}} \rightarrow{dt}=\mathrm{2}{udu} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{u}\sqrt{{u}^{\mathrm{2}} }}{\mathrm{1}+{u}^{\mathrm{4}} }{du}\rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{4}} }{du} \\ $$$${let}\:{z}={u}^{\mathrm{4}} \overset{{u}={z}^{\frac{\mathrm{1}}{\mathrm{4}}} } {\rightarrow}{dz}=\mathrm{4}{u}^{\mathrm{3}} \Rightarrow{du}=\frac{{dz}}{\mathrm{4}{u}^{\mathrm{3}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{u}^{\mathrm{2}} .{u}^{−\mathrm{3}} }{\mathrm{4}\left(\mathrm{1}+{z}\right)}{dz}\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{z}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{1}+{z}\right)}{dz} \\ $$$${using}\:\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{m}−\mathrm{1}} }{\left(\mathrm{1}+{x}\right)^{{m}+{n}} }{dx}\rightarrow\Gamma\left({m}\right)\Gamma\left({n}\right) \\ $$$${m}=\frac{\mathrm{3}}{\mathrm{4}}\:\:{amd}\:{n}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\right)=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{2}\pi}{\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$Kudos to my Mentors: Prempeh (Euclid)🇬🇭 and to Daniel (Small Einstein)🇳🇬
Answered by Mathspace last updated on 17/Apr/22
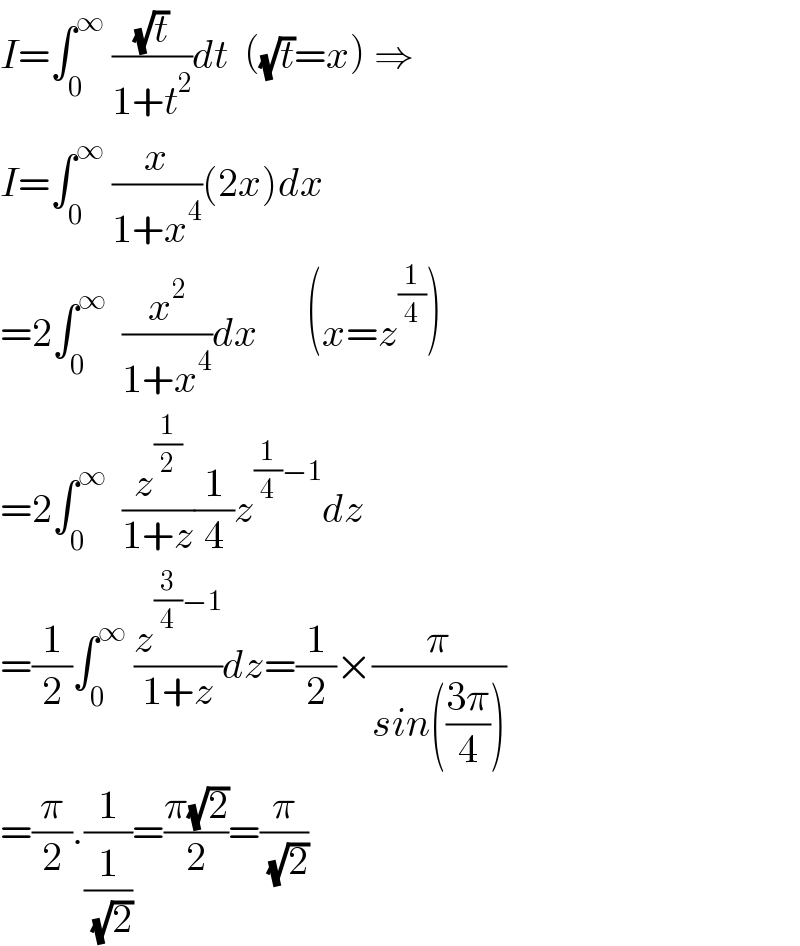
$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\sqrt{{t}}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\left(\sqrt{{t}}={x}\right)\:\Rightarrow \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{4}} }\left(\mathrm{2}{x}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx}\:\:\:\:\:\:\left({x}={z}^{\frac{\mathrm{1}}{\mathrm{4}}} \right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{z}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{z}}\frac{\mathrm{1}}{\mathrm{4}}{z}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} {dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{{z}^{\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{z}}{dz}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)} \\ $$$$=\frac{\pi}{\mathrm{2}}.\frac{\mathrm{1}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
