Menu Close

0-tan-1-x-4-tan-1-x-6-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 117213 by bobhans last updated on 10/Oct/20
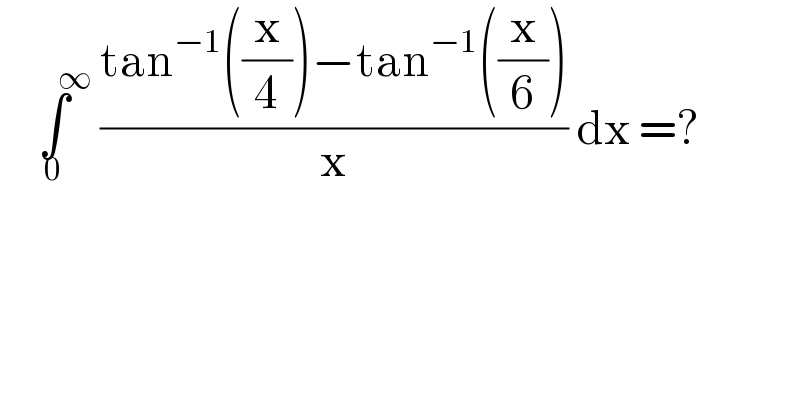
∫_0 ^( ∞) ((tan^(−1) ((x/4))−tan^(−1) ((x/6)))/x) dx =?
$$\:\:\underset{\mathrm{0}} {\overset{\:\:\:\:\:\:\:\infty} {\int}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{4}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{6}}\right)}{\mathrm{x}}\:\mathrm{dx}\:=? \\ $$
Answered by TANMAY PANACEA last updated on 10/Oct/20
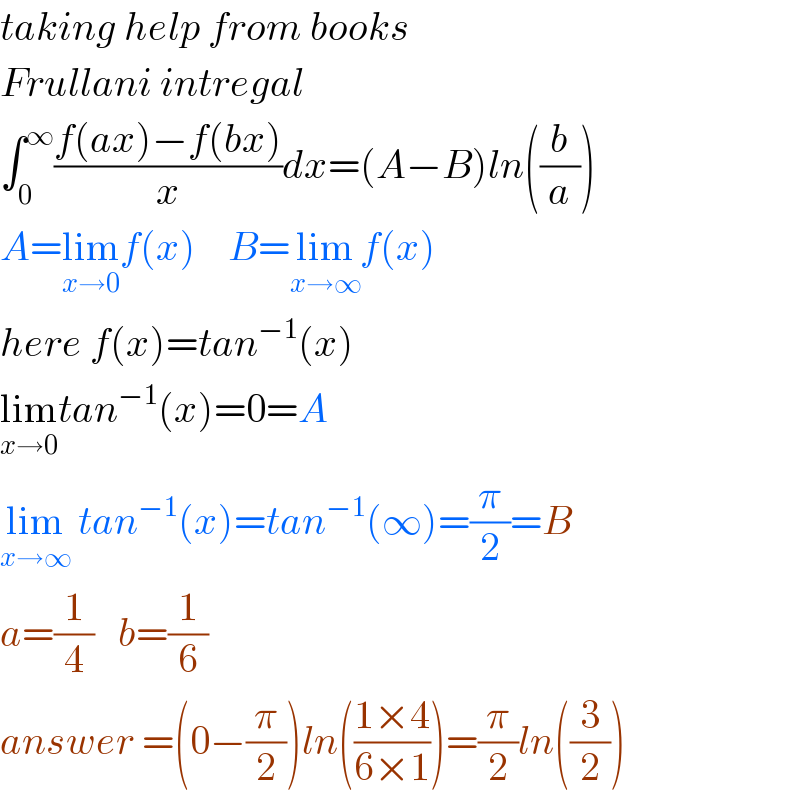
taking help from books Frullani intregal ∫_0 ^∞ ((f(ax)−f(bx))/x)dx=(A−B)ln((b/a)) A=lim_(x→0) f(x) B=lim_(x→∞) f(x) here f(x)=tan^(−1) (x) lim_(x→0) tan^(−1) (x)=0=A lim_(x→∞) tan^(−1) (x)=tan^(−1) (∞)=(π/2)=B a=(1/4) b=(1/6) answer =(0−(π/2))ln(((1×4)/(6×1)))=(π/2)ln((3/2))
$${taking}\:{help}\:{from}\:{books} \\ $$$${Frullani}\:{intregal} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{f}\left({ax}\right)−{f}\left({bx}\right)}{{x}}{dx}=\left({A}−{B}\right){ln}\left(\frac{{b}}{{a}}\right) \\ $$$${A}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)\:\:\:\:{B}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right) \\ $$$${here}\:{f}\left({x}\right)={tan}^{−\mathrm{1}} \left({x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{tan}^{−\mathrm{1}} \left({x}\right)=\mathrm{0}={A} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{tan}^{−\mathrm{1}} \left({x}\right)={tan}^{−\mathrm{1}} \left(\infty\right)=\frac{\pi}{\mathrm{2}}={B} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{4}}\:\:\:{b}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${answer}\:=\left(\mathrm{0}−\frac{\pi}{\mathrm{2}}\right){ln}\left(\frac{\mathrm{1}×\mathrm{4}}{\mathrm{6}×\mathrm{1}}\right)=\frac{\pi}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by bobhans last updated on 10/Oct/20
waw....do you have that book?
$$\mathrm{waw}….\mathrm{do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{that}\:\mathrm{book}? \\ $$
Commented by TANMAY PANACEA last updated on 10/Oct/20
yes sir...hard copy...i do not know how to share image or documents in pdf form
$${yes}\:{sir}…{hard}\:{copy}…{i}\:{do}\:{not}\:{know}\:{how}\:{to}\:{share}\:{image} \\ $$$${or}\:{documents}\:{in}\:{pdf}\:{form} \\ $$
Commented by bemath last updated on 10/Oct/20
may be sir can sent by gmail
$${may}\:{be}\:{sir}\:{can}\:{sent}\:{by}\:{gmail} \\ $$
Answered by AbduraufKodiriy last updated on 10/Oct/20
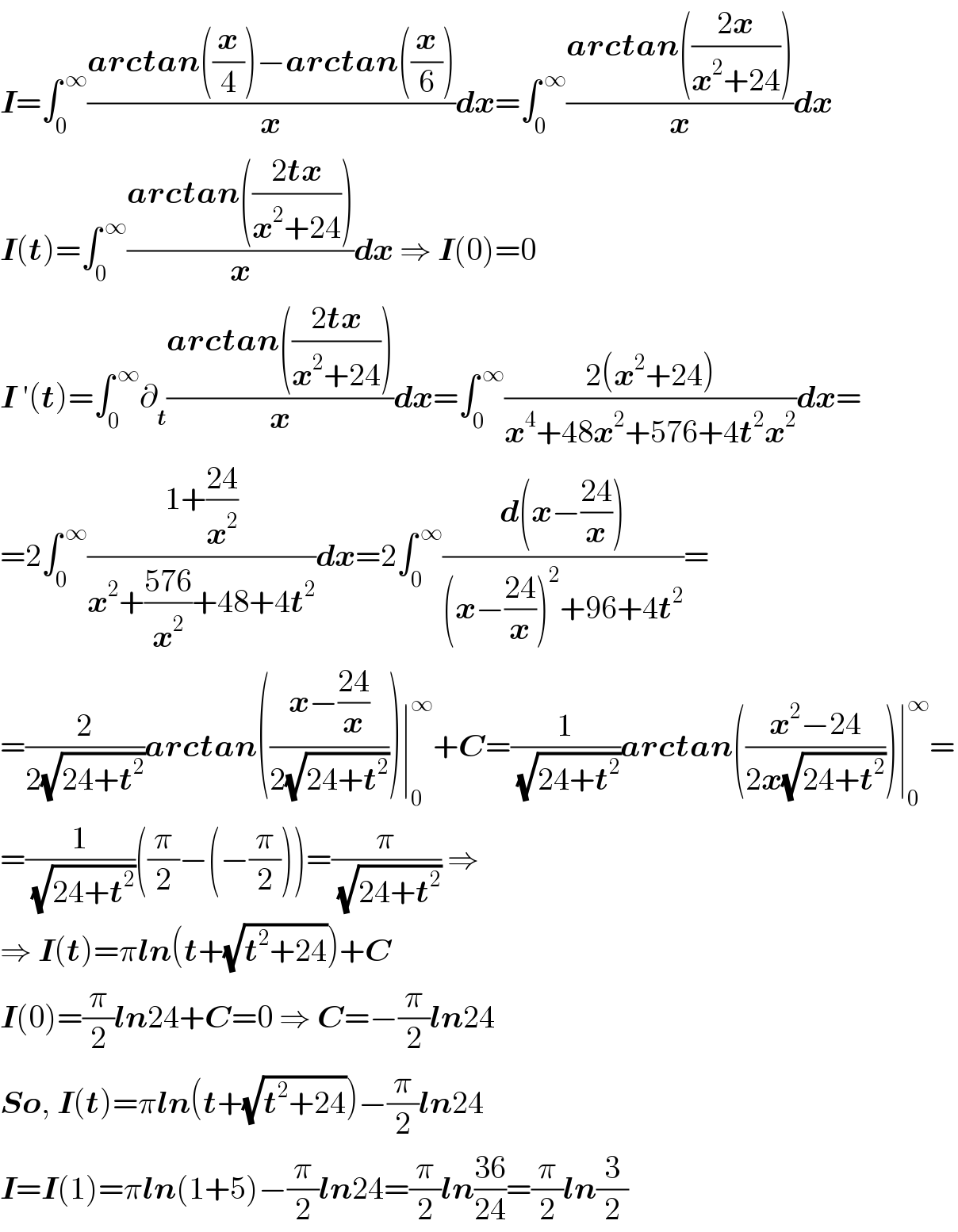
I=∫_0 ^( ∞) ((arctan((x/4))−arctan((x/6)))/x)dx=∫_0 ^( ∞) ((arctan(((2x)/(x^2 +24))))/x)dx I(t)=∫_0 ^( ∞) ((arctan(((2tx)/(x^2 +24))))/x)dx ⇒ I(0)=0 I ′(t)=∫_0 ^( ∞) ∂_t ((arctan(((2tx)/(x^2 +24))))/x)dx=∫_0 ^( ∞) ((2(x^2 +24))/(x^4 +48x^2 +576+4t^2 x^2 ))dx= =2∫_0 ^( ∞) ((1+((24)/x^2 ))/(x^2 +((576)/x^2 )+48+4t^2 ))dx=2∫_0 ^( ∞) ((d(x−((24)/x)))/((x−((24)/x))^2 +96+4t^2 ))= =(2/(2(√(24+t^2 ))))arctan(((x−((24)/x))/(2(√(24+t^2 )))))∣_0 ^∞ +C=(1/( (√(24+t^2 ))))arctan(((x^2 −24)/(2x(√(24+t^2 )))))∣_0 ^∞ = =(1/( (√(24+t^2 ))))((π/2)−(−(π/2)))=(π/( (√(24+t^2 )))) ⇒ ⇒ I(t)=πln(t+(√(t^2 +24)))+C I(0)=(π/2)ln24+C=0 ⇒ C=−(π/2)ln24 So, I(t)=πln(t+(√(t^2 +24)))−(π/2)ln24 I=I(1)=πln(1+5)−(π/2)ln24=(π/2)ln((36)/(24))=(π/2)ln(3/2)
$$\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\:\infty} \frac{\boldsymbol{{arctan}}\left(\frac{\boldsymbol{{x}}}{\mathrm{4}}\right)−\boldsymbol{{arctan}}\left(\frac{\boldsymbol{{x}}}{\mathrm{6}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}}=\int_{\mathrm{0}} ^{\:\infty} \frac{\boldsymbol{{arctan}}\left(\frac{\mathrm{2}\boldsymbol{{x}}}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{24}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}} \\ $$$$\boldsymbol{{I}}\left(\boldsymbol{{t}}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{\boldsymbol{{arctan}}\left(\frac{\mathrm{2}\boldsymbol{{tx}}}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{24}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}}\:\Rightarrow\:\boldsymbol{{I}}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\boldsymbol{{I}}\:'\left(\boldsymbol{{t}}\right)=\int_{\mathrm{0}} ^{\:\infty} \partial_{\boldsymbol{{t}}} \frac{\boldsymbol{{arctan}}\left(\frac{\mathrm{2}\boldsymbol{{tx}}}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{24}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}}=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2}\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{24}\right)}{\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{48}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{576}+\mathrm{4}\boldsymbol{{t}}^{\mathrm{2}} \boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}}= \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}+\frac{\mathrm{24}}{\boldsymbol{{x}}^{\mathrm{2}} }}{\boldsymbol{{x}}^{\mathrm{2}} +\frac{\mathrm{576}}{\boldsymbol{{x}}^{\mathrm{2}} }+\mathrm{48}+\mathrm{4}\boldsymbol{{t}}^{\mathrm{2}} }\boldsymbol{{dx}}=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\boldsymbol{{d}}\left(\boldsymbol{{x}}−\frac{\mathrm{24}}{\boldsymbol{{x}}}\right)}{\left(\boldsymbol{{x}}−\frac{\mathrm{24}}{\boldsymbol{{x}}}\right)^{\mathrm{2}} +\mathrm{96}+\mathrm{4}\boldsymbol{{t}}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{24}+\boldsymbol{{t}}^{\mathrm{2}} }}\boldsymbol{{arctan}}\left(\frac{\boldsymbol{{x}}−\frac{\mathrm{24}}{\boldsymbol{{x}}}}{\mathrm{2}\sqrt{\mathrm{24}+\boldsymbol{{t}}^{\mathrm{2}} }}\right)\mid_{\mathrm{0}} ^{\infty} +\boldsymbol{{C}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{24}+\boldsymbol{{t}}^{\mathrm{2}} }}\boldsymbol{{arctan}}\left(\frac{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{24}}{\mathrm{2}\boldsymbol{{x}}\sqrt{\mathrm{24}+\boldsymbol{{t}}^{\mathrm{2}} }}\right)\mid_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{24}+\boldsymbol{{t}}^{\mathrm{2}} }}\left(\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)\right)=\frac{\pi}{\:\sqrt{\mathrm{24}+\boldsymbol{{t}}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\Rightarrow\:\boldsymbol{{I}}\left(\boldsymbol{{t}}\right)=\pi\boldsymbol{{ln}}\left(\boldsymbol{{t}}+\sqrt{\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{24}}\right)+\boldsymbol{{C}} \\ $$$$\boldsymbol{{I}}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{2}}\boldsymbol{{ln}}\mathrm{24}+\boldsymbol{{C}}=\mathrm{0}\:\Rightarrow\:\boldsymbol{{C}}=−\frac{\pi}{\mathrm{2}}\boldsymbol{{ln}}\mathrm{24} \\ $$$$\boldsymbol{{So}},\:\boldsymbol{{I}}\left(\boldsymbol{{t}}\right)=\pi\boldsymbol{{ln}}\left(\boldsymbol{{t}}+\sqrt{\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{24}}\right)−\frac{\pi}{\mathrm{2}}\boldsymbol{{ln}}\mathrm{24} \\ $$$$\boldsymbol{{I}}=\boldsymbol{{I}}\left(\mathrm{1}\right)=\pi\boldsymbol{{ln}}\left(\mathrm{1}+\mathrm{5}\right)−\frac{\pi}{\mathrm{2}}\boldsymbol{{ln}}\mathrm{24}=\frac{\pi}{\mathrm{2}}\boldsymbol{{ln}}\frac{\mathrm{36}}{\mathrm{24}}=\frac{\pi}{\mathrm{2}}\boldsymbol{{ln}}\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 10/Oct/20
I =∫_0 ^∞ ((arctan(ax)−arctan(bx))/x)dx =limI(ξ)with I(ξ)=∫_0 ^ξ ((arctan(ax)−arctan(bx))/x)dx=I ∫_0 ^∞ (...)dx =lim_(ξ→+∞) I(ξ) I(ξ) =∫_0 ^ξ ((arctan(ax))/x)dx(→ax =u)−∫_0 ^ξ ((arctan(bx))/x)dx(bx=v) =∫_0 ^(aξ) ((arctanu)/u)du −∫_0 ^(bξ) ((arctanv)/v)dv =∫_(bξ) ^(aξ) ((arctan(u))/u)du ∃ c ∈]bξ ,aξ[ / ∫_(bξ) ^(aξ) ((arctan(u))/u)du =arctanc ∫_(bξ) ^(aξ) (du/u) =arctancln((a/b)) ⇒lim_(ξ→+∞) I(ξ) =(π/2)ln((a/b)) with a=(1/4) and b=(1/6) ⇒(a/b)=(6/4)=(3/2) ⇒∫_0 ^∞ ((arctan((x/4))−arctan((x/6)))/x)dx =(π/2)ln((3/2))
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{ax}\right)−\mathrm{arctan}\left(\mathrm{bx}\right)}{\mathrm{x}}\mathrm{dx}\:=\mathrm{limI}\left(\xi\right)\mathrm{with}\:\:\mathrm{I}\left(\xi\right)=\int_{\mathrm{0}} ^{\xi} \:\frac{\mathrm{arctan}\left(\mathrm{ax}\right)−\mathrm{arctan}\left(\mathrm{bx}\right)}{\mathrm{x}}\mathrm{dx}=\mathrm{I} \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(…\right)\mathrm{dx}\:=\mathrm{lim}_{\xi\rightarrow+\infty} \mathrm{I}\left(\xi\right) \\ $$$$\mathrm{I}\left(\xi\right)\:=\int_{\mathrm{0}} ^{\xi} \:\frac{\mathrm{arctan}\left(\mathrm{ax}\right)}{\mathrm{x}}\mathrm{dx}\left(\rightarrow\mathrm{ax}\:=\mathrm{u}\right)−\int_{\mathrm{0}} ^{\xi} \:\frac{\mathrm{arctan}\left(\mathrm{bx}\right)}{\mathrm{x}}\mathrm{dx}\left(\mathrm{bx}=\mathrm{v}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{a}\xi} \:\frac{\mathrm{arctanu}}{\mathrm{u}}\mathrm{du}\:−\int_{\mathrm{0}} ^{\mathrm{b}\xi} \:\frac{\mathrm{arctanv}}{\mathrm{v}}\mathrm{dv}\:=\int_{\mathrm{b}\xi} ^{\mathrm{a}\xi} \:\frac{\mathrm{arctan}\left(\mathrm{u}\right)}{\mathrm{u}}\mathrm{du} \\ $$$$\left.\exists\:\mathrm{c}\:\in\right]\mathrm{b}\xi\:,\mathrm{a}\xi\left[\:\:/\:\int_{\mathrm{b}\xi} ^{\mathrm{a}\xi} \:\frac{\mathrm{arctan}\left(\mathrm{u}\right)}{\mathrm{u}}\mathrm{du}\:=\mathrm{arctanc}\:\int_{\mathrm{b}\xi} ^{\mathrm{a}\xi} \:\frac{\mathrm{du}}{\mathrm{u}}\:=\mathrm{arctancln}\left(\frac{\mathrm{a}}{\mathrm{b}}\right)\right. \\ $$$$\Rightarrow\mathrm{lim}_{\xi\rightarrow+\infty} \mathrm{I}\left(\xi\right)\:=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{a}}{\mathrm{b}}\right)\:\:\mathrm{with}\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{and}\:\mathrm{b}=\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{4}}\right)−\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{6}}\right)}{\mathrm{x}}\mathrm{dx}\:=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *