Question Number 144187 by ArielVyny last updated on 22/Jun/21
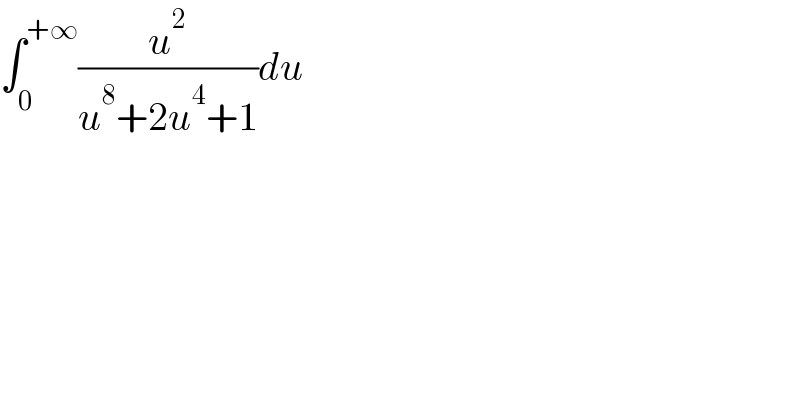
$$\int_{\mathrm{0}} ^{+\infty} \frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{8}} +\mathrm{2}{u}^{\mathrm{4}} +\mathrm{1}}{du} \\ $$
Answered by Ar Brandon last updated on 22/Jun/21

$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{8}} +\mathrm{2u}^{\mathrm{4}} +\mathrm{1}}\mathrm{du}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\mathrm{2}} }{\left(\mathrm{u}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{4}}} }{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}}\beta\left(\frac{\mathrm{3}}{\mathrm{4}},\frac{\mathrm{5}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{16}}\beta\left(\frac{\mathrm{3}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{16}}\centerdot\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\sqrt{\mathrm{2}}\pi}{\mathrm{16}} \\ $$
