Question Number 27447 by raman last updated on 07/Jan/18
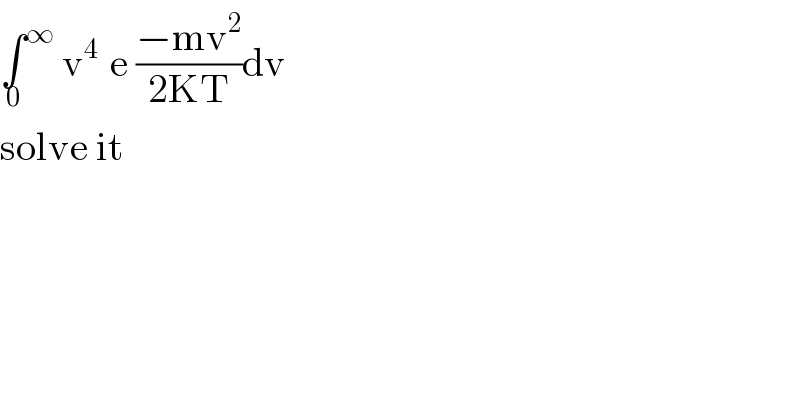
$$\underset{\mathrm{0}} {\int}^{\infty} \:\mathrm{v}^{\mathrm{4}\:} \:\mathrm{e}\:\frac{−\mathrm{mv}^{\mathrm{2}} }{\mathrm{2KT}}\mathrm{dv}\: \\ $$$$\mathrm{solve}\:\mathrm{it} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/May/18
![let x=(m/(2KT))v^2 v=((√(2KT))/( (√m))) ×x^(1/2) dx=(m/(2KT))×2v dv =(m/(KT))×((√(2KT))/( (√m)))×x_ ^(1/2) dv so dv=((KT)/m)×(((√m) )/( (√(2KT))))×x^(−(1/2)) × dx(/) ∫_0 ^∞ (((2KT)^2 )/m^2 )×x^2 ×e^(−x) ×((√(KT))/( (√m) ))×(1/( (√2)))×x^((−1)/2) ×dx ∫_0 ^∞ ((2^(3/2) ×(KT)^(5/2) )/m^(5/2) )e^(−x) ×x^(3/2) ×dx =[((8(KT)^5 )/m^5 )]^(1/2) ×∫_0 ^∞ e^(−x) ×x^(3/2) dx =ditto×⌈((5/2)) { ∫_0 ^∞ e^(−x) ×x^(n−1) =⌈(n)} now ⌈((5/2))=(3/2)×(1/2)×(√Π) ={((8(KT)^5 )/m^5 )}^(1/2) ×(3/4)×(√Π) pls check](https://www.tinkutara.com/question/Q35557.png)
$${let}\:{x}=\frac{{m}}{\mathrm{2}{KT}}{v}^{\mathrm{2}} \:\:\:{v}=\frac{\sqrt{\mathrm{2}{KT}}}{\:\sqrt{{m}}}\:\:\:×{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${dx}=\frac{{m}}{\mathrm{2}{KT}}×\mathrm{2}{v}\:{dv} \\ $$$$=\frac{{m}}{{KT}}×\frac{\sqrt{\mathrm{2}{KT}}}{\:\sqrt{{m}}}×{x}_{} ^{\frac{\mathrm{1}}{\mathrm{2}}} {dv}\:\:{so}\:{dv}=\frac{{KT}}{{m}}×\frac{\sqrt{{m}}\:}{\:\sqrt{\mathrm{2}{KT}}}×{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} × \\ $$$${dx}\frac{}{} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{2}{KT}\right)^{\mathrm{2}} }{{m}^{\mathrm{2}} }×{x}^{\mathrm{2}} ×{e}^{−{x}} ×\frac{\sqrt{{KT}}}{\:\sqrt{{m}}\:}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×{x}^{\frac{−\mathrm{1}}{\mathrm{2}}} \:×{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \:×\left({KT}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} }{{m}^{\frac{\mathrm{5}}{\mathrm{2}}} }{e}^{−{x}} ×{x}^{\frac{\mathrm{3}}{\mathrm{2}}} ×{dx} \\ $$$$=\left[\frac{\mathrm{8}\left({KT}\right)^{\mathrm{5}} }{{m}^{\mathrm{5}} }\right]^{\frac{\mathrm{1}}{\mathrm{2}}} ×\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} ×{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:{dx} \\ $$$$={ditto}×\lceil\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:\:\:\left\{\:\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} ×{x}^{{n}−\mathrm{1}} =\lceil\left({n}\right)\right\} \\ $$$${now}\:\lceil\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\Pi}\:\: \\ $$$$=\left\{\frac{\mathrm{8}\left({KT}\right)^{\mathrm{5}} }{{m}^{\mathrm{5}} }\right\}^{\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{3}}{\mathrm{4}}×\sqrt{\Pi}\:\: \\ $$$${pls}\:{check} \\ $$$$ \\ $$
