Question Number 62937 by Prithwish sen last updated on 27/Jun/19

$$\int_{\mathrm{0}} ^{\:\:\mathrm{x}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 27/Jun/19
![∫_0 ^x (dt/(1+t^2 )) =[arctan(t)]_0 ^x =arctanx .](https://www.tinkutara.com/question/Q62967.png)
$$\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\left[{arctan}\left({t}\right)\right]_{\mathrm{0}} ^{{x}} \:={arctanx}\:. \\ $$
Commented by Prithwish sen last updated on 27/Jun/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Prithwish sen last updated on 27/Jun/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by peter frank last updated on 27/Jun/19
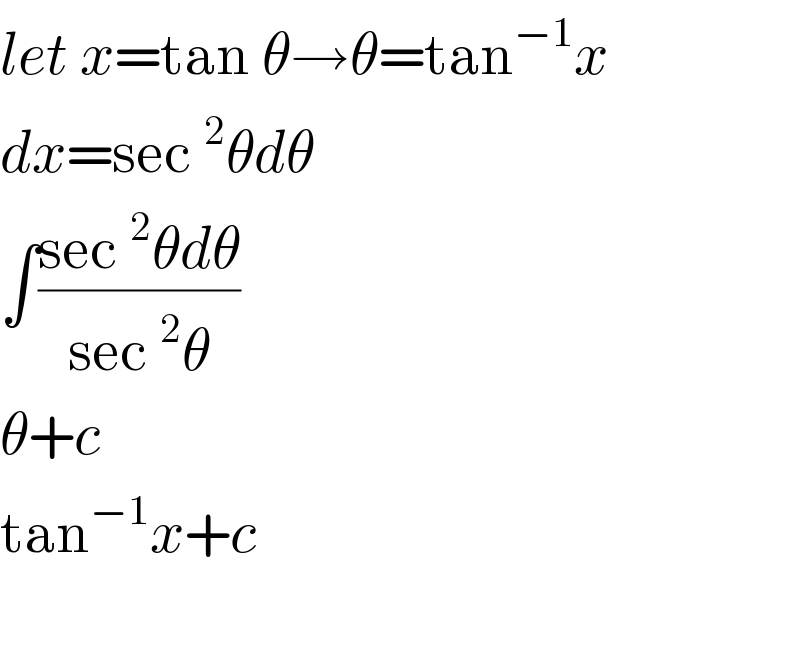
$${let}\:{x}=\mathrm{tan}\:\theta\rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} {x} \\ $$$${dx}=\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\int\frac{\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{sec}\:^{\mathrm{2}} \theta} \\ $$$$\theta+{c} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}+{c} \\ $$$$ \\ $$
Commented by Prithwish sen last updated on 27/Jun/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
