Question Number 191631 by Spillover last updated on 27/Apr/23
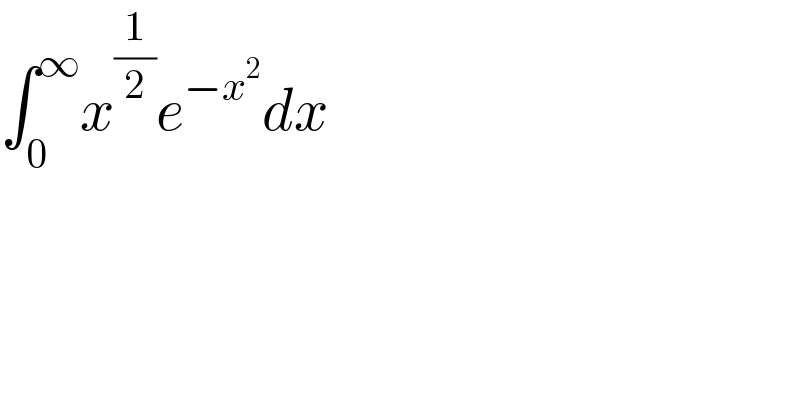
$$\int_{\mathrm{0}} ^{\infty} {x}^{\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{x}^{\mathrm{2}} } {dx} \\ $$
Answered by malwan last updated on 28/Apr/23

$${put}\:{x}^{\mathrm{2}} ={y}\Rightarrow{x}={y}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\therefore\:\:_{\mathrm{0}} \int^{\:\infty} {y}^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{−{y}} \left(\frac{\mathrm{1}}{\mathrm{2}}\:{y}^{−\frac{\mathrm{1}}{\mathrm{2}}} {dy}\right) \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:_{\mathrm{0}} \int^{\:\infty} {y}^{\:−\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{−{y}} {dy} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\Gamma\left(−\frac{\mathrm{1}}{\mathrm{4}}\:+\:\mathrm{1}\right)}{\mathrm{1}^{−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}} }\:=\:\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\mathrm{2}} \\ $$$${Mohammed}\:{Alwan} \\ $$$$\mathrm{28}/\mathrm{4}/\mathrm{2023} \\ $$
Commented by Spillover last updated on 28/Apr/23

$${thanks} \\ $$
