Question Number 127420 by liberty last updated on 29/Dec/20
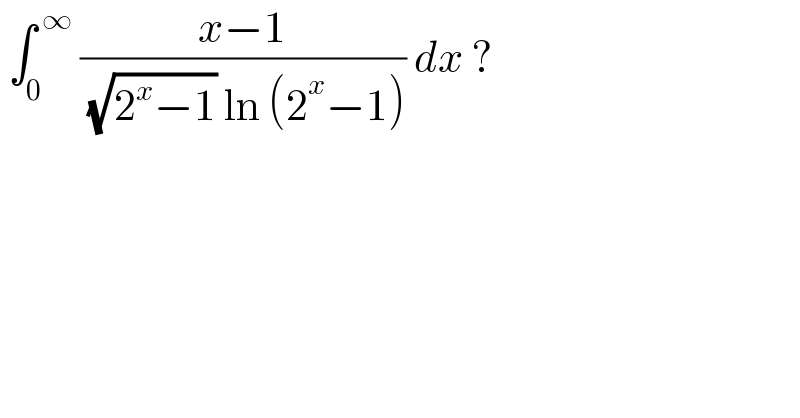
$$\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{x}−\mathrm{1}}{\:\sqrt{\mathrm{2}^{{x}} −\mathrm{1}}\:\mathrm{ln}\:\left(\mathrm{2}^{{x}} −\mathrm{1}\right)}\:{dx}\:? \\ $$
Answered by mnjuly1970 last updated on 29/Dec/20
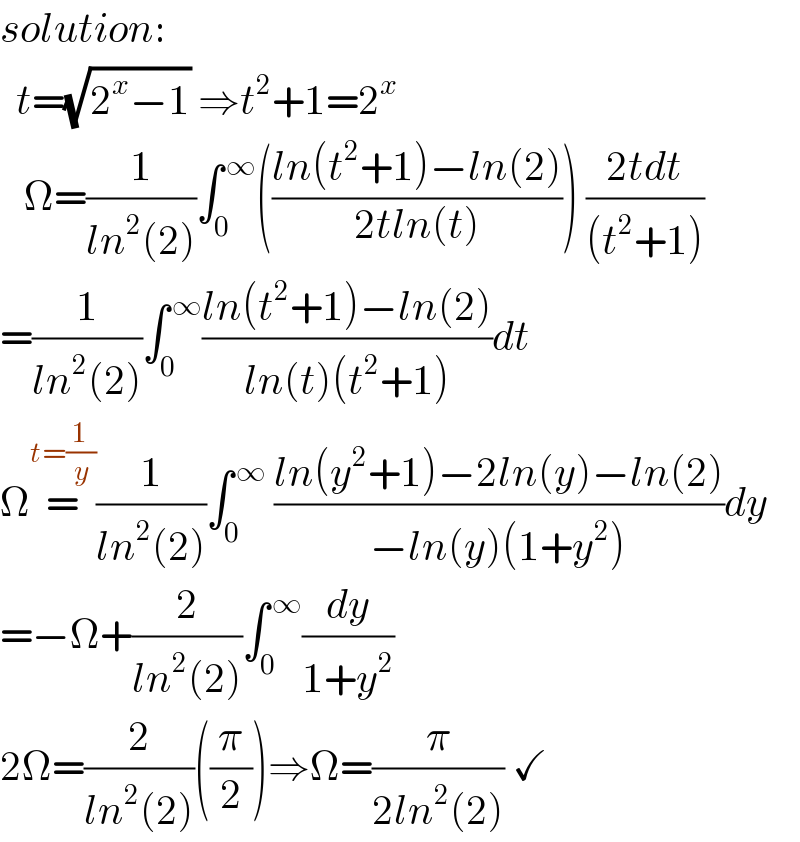
$${solution}: \\ $$$$\:\:{t}=\sqrt{\mathrm{2}^{{x}} −\mathrm{1}}\:\Rightarrow{t}^{\mathrm{2}} +\mathrm{1}=\mathrm{2}^{{x}} \\ $$$$\:\:\:\Omega=\frac{\mathrm{1}}{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{ln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−{ln}\left(\mathrm{2}\right)}{\mathrm{2}{tln}\left({t}\right)}\right)\:\frac{\mathrm{2}{tdt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−{ln}\left(\mathrm{2}\right)}{{ln}\left({t}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt} \\ $$$$\Omega\overset{{t}=\frac{\mathrm{1}}{{y}}} {=}\frac{\mathrm{1}}{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\:\infty} \:\frac{{ln}\left({y}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2}{ln}\left({y}\right)−{ln}\left(\mathrm{2}\right)}{−{ln}\left({y}\right)\left(\mathrm{1}+{y}^{\mathrm{2}} \right)}{dy} \\ $$$$=−\Omega+\frac{\mathrm{2}}{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\:\infty} \frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$$\mathrm{2}\Omega=\frac{\mathrm{2}}{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}\left(\frac{\pi}{\mathrm{2}}\right)\Rightarrow\Omega=\frac{\pi}{\mathrm{2}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}\:\checkmark \\ $$
Commented by liberty last updated on 30/Dec/20
sabiħ ... grazzi għat-tlestija tiegħek
