Question Number 126904 by Mustafa2020 last updated on 25/Dec/20
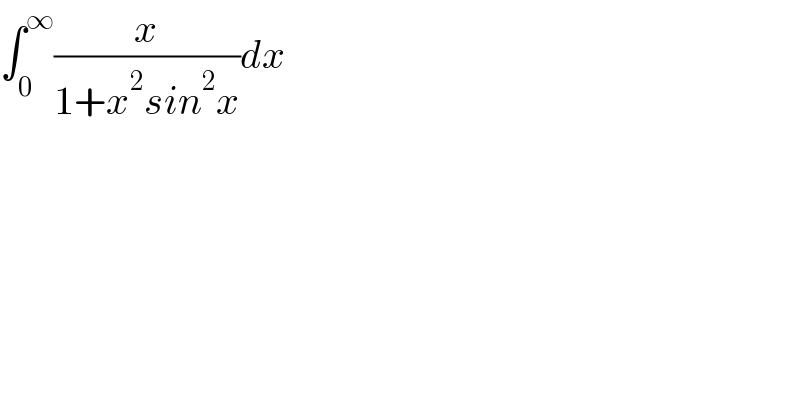
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}{dx} \\ $$
Answered by mindispower last updated on 25/Dec/20

$$\geqslant\Sigma\int_{\mathrm{2}{k}\pi} ^{\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{6}}} \frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} {sin}^{\mathrm{2}} \left({x}\right)}{dx}\geqslant\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{2}{k}\pi\right)}{\mathrm{1}+\left(\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{6}}\right)^{\mathrm{2}} .\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${wich}\:{diverge}\:\sim\frac{\mathrm{1}}{\mathrm{2}\pi{k}}\:{harmonic}\:{serie} \\ $$$$ \\ $$
