Menu Close

0-x-2-1-x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 123998 by john_santu last updated on 30/Nov/20
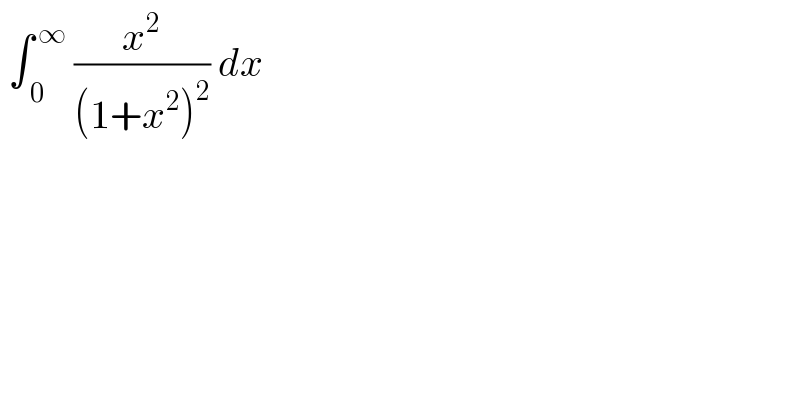
∫_( 0) ^( ∞) (x^2 /((1+x^2 )^2 )) dx
$$\:\int_{\:\mathrm{0}} ^{\:\infty} \:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\: \\ $$
Answered by liberty last updated on 30/Nov/20
substituting x = tan q with upper limit (π/2) and lower limit 0 ∫_( 0) ^( π/2) ((tan^2 q .sec^2 q dq)/(sec^4 q)) = ∫_( 0 ) ^( π/2) sin^2 q dq = ∫_( 0) ^( π/2) ((1/2)−(1/2)cos 2q )dq = [(1/2)q−(1/4)sin 2q ]_( 0) ^(π/2) = (π/4).
$$\:{substituting}\:{x}\:=\:\mathrm{tan}\:{q}\:{with}\:{upper}\:{limit}\:\frac{\pi}{\mathrm{2}} \\ $$$${and}\:{lower}\:{limit}\:\mathrm{0} \\ $$$$\int_{\:\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{tan}\:^{\mathrm{2}} {q}\:.\mathrm{sec}\:^{\mathrm{2}} {q}\:{dq}}{\mathrm{sec}\:^{\mathrm{4}} {q}}\:=\:\int_{\:\mathrm{0}\:} ^{\:\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {q}\:{dq}\: \\ $$$$\:=\:\int_{\:\mathrm{0}} ^{\:\pi/\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{q}\:\right){dq}\:=\:\left[\frac{\mathrm{1}}{\mathrm{2}}{q}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{q}\:\right]_{\:\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$\:=\:\frac{\pi}{\mathrm{4}}. \\ $$
Answered by Dwaipayan Shikari last updated on 30/Nov/20
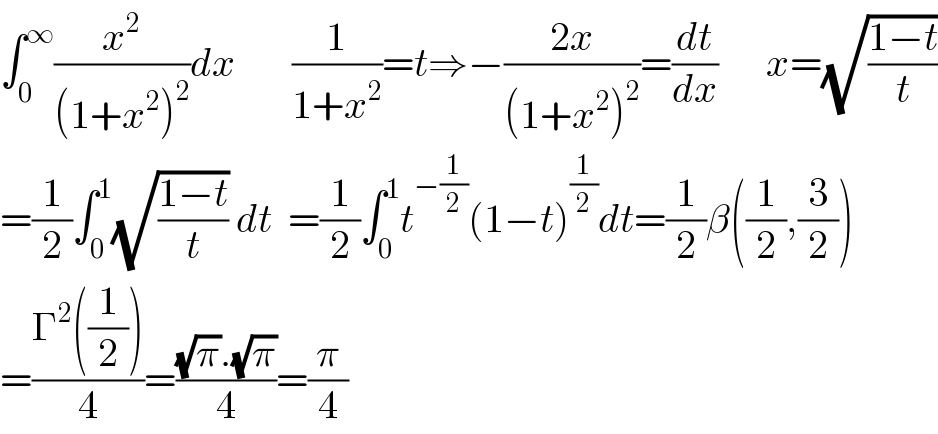
∫_0 ^∞ (x^2 /((1+x^2 )^2 ))dx (1/(1+x^2 ))=t⇒−((2x)/((1+x^2 )^2 ))=(dt/dx) x=(√((1−t)/t)) =(1/2)∫_0 ^1 (√((1−t)/t)) dt =(1/2)∫_0 ^1 t^(−(1/2)) (1−t)^(1/2) dt=(1/2)β((1/2),(3/2)) =((Γ^2 ((1/2)))/4)=(((√π).(√π))/4)=(π/4)
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }={t}\Rightarrow−\frac{\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{{dt}}{{dx}}\:\:\:\:\:\:{x}=\sqrt{\frac{\mathrm{1}−{t}}{{t}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−{t}}{{t}}}\:{dt}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{4}}=\frac{\sqrt{\pi}.\sqrt{\pi}}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 30/Nov/20
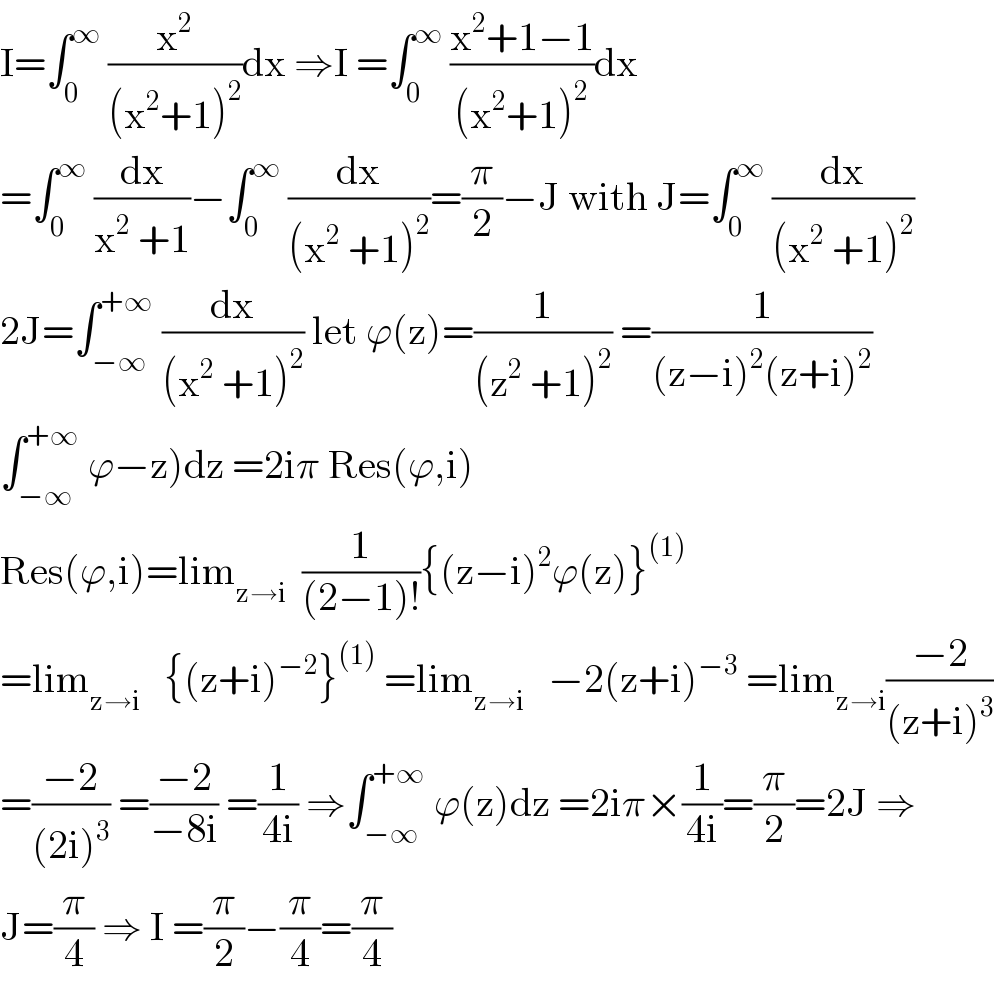
I=∫_0 ^∞ (x^2 /((x^2 +1)^2 ))dx ⇒I =∫_0 ^∞ ((x^2 +1−1)/((x^2 +1)^2 ))dx =∫_0 ^∞ (dx/(x^2 +1))−∫_0 ^∞ (dx/((x^2 +1)^2 ))=(π/2)−J with J=∫_0 ^∞ (dx/((x^2 +1)^2 )) 2J=∫_(−∞) ^(+∞) (dx/((x^2 +1)^2 )) let ϕ(z)=(1/((z^2 +1)^2 )) =(1/((z−i)^2 (z+i)^2 )) ∫_(−∞) ^(+∞) ϕ−z)dz =2iπ Res(ϕ,i) Res(ϕ,i)=lim_(z→i) (1/((2−1)!)){(z−i)^2 ϕ(z)}^((1)) =lim_(z→i) {(z+i)^(−2) }^((1)) =lim_(z→i) −2(z+i)^(−3) =lim_(z→i) ((−2)/((z+i)^3 )) =((−2)/((2i)^3 )) =((−2)/(−8i)) =(1/(4i)) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ×(1/(4i))=(π/2)=2J ⇒ J=(π/4) ⇒ I =(π/2)−(π/4)=(π/4)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}}−\mathrm{J}\:\mathrm{with}\:\mathrm{J}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2J}=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\left.\int_{−\infty} ^{+\infty} \:\varphi−\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{2}} \right\}^{\left(\mathrm{1}\right)} \:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:−\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{3}} \:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \frac{−\mathrm{2}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{2}}{\left(\mathrm{2i}\right)^{\mathrm{3}} }\:=\frac{−\mathrm{2}}{−\mathrm{8i}}\:=\frac{\mathrm{1}}{\mathrm{4i}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\mathrm{1}}{\mathrm{4i}}=\frac{\pi}{\mathrm{2}}=\mathrm{2J}\:\Rightarrow \\ $$$$\mathrm{J}=\frac{\pi}{\mathrm{4}}\:\Rightarrow\:\mathrm{I}\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$
Answered by mnjuly1970 last updated on 01/Dec/20
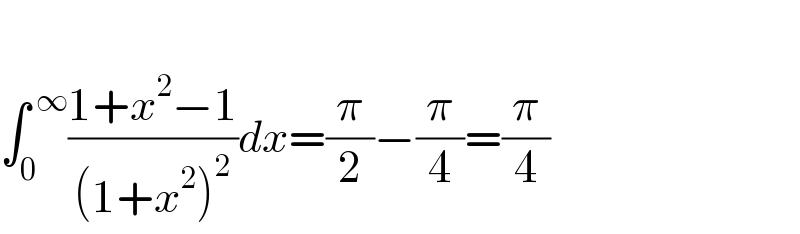
∫_0 ^( ∞) ((1+x^2 −1)/((1+x^2 )^2 ))dx=(π/2)−(π/4)=(π/4)
$$ \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *