Menu Close

0-x-2-2-x-4-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 118307 by bramlexs22 last updated on 16/Oct/20
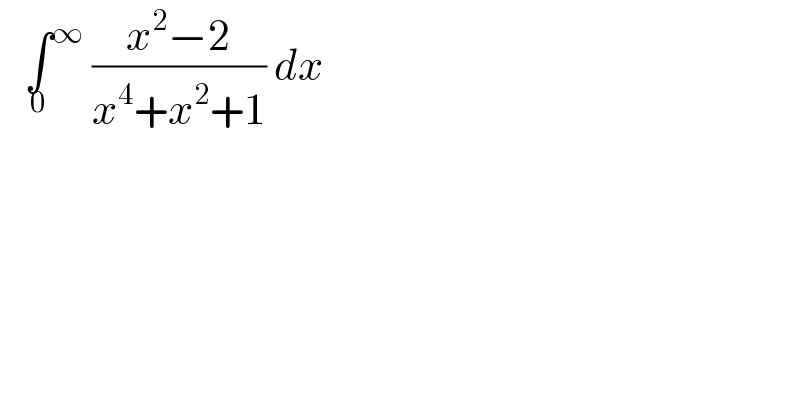
∫^∞ _0 ((x^2 −2)/(x^4 +x^2 +1)) dx
$$\:\:\:\underset{\mathrm{0}} {\int}^{\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$
Commented by Lordose last updated on 16/Oct/20
see qst 118030
$$\mathrm{see}\:\mathrm{qst}\:\mathrm{118030} \\ $$
Answered by TANMAY PANACEA last updated on 16/Oct/20
∫((x^2 −2)/(x^4 +x^2 +1))dx ∫(dx/(x^2 +1+(1/x^2 )))−∫((2/x^2 )/(x^2 +1+(1/x^2 )))dx (1/2)∫((1+(1/x^2 )+1−(1/x^2 ))/(x^2 +(1/x^2 )+1))−∫((1+(1/x^2 )−(1−(1/x^2 )))/(x^2 +(1/x^2 )+1)) (1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +3))+(1/2)∫((d(x+(1/x)))/((x+(1/x))^2 −1))−∫((d(x−(1/x)))/((x−(1/x))^2 +3))+∫((d(x+(1/x)))/((x+(1/x))^2 −1)) (3/2)∫((d(x+(1/x)))/((x+(1/x))^2 −1))(1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +3)) now pls use formula ∫(dy/(y^2 −a^2 )) and ∫(dy/(y^2 +a^2 )) and put limit pls i prefer not to remember formula rather i like how formula is derived
$$\int\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}−\int\frac{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}−\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}}−\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}+\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}}\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{pls}}\:\boldsymbol{{use}}\:\boldsymbol{{formula}} \\ $$$$\int\frac{{dy}}{{y}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:{and}\:\int\frac{{dy}}{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\:\:{and}\:{put}\:{limit}\:{pls} \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{prefer}}\:\boldsymbol{{not}}\:\boldsymbol{{to}}\:\boldsymbol{{remember}}\:\boldsymbol{{formula}} \\ $$$$\boldsymbol{{rather}}\:\boldsymbol{{i}}\:\boldsymbol{{like}}\:\boldsymbol{{how}}\:\boldsymbol{{formula}}\:\boldsymbol{{is}}\:\boldsymbol{{derived}} \\ $$
Answered by Bird last updated on 17/Oct/20
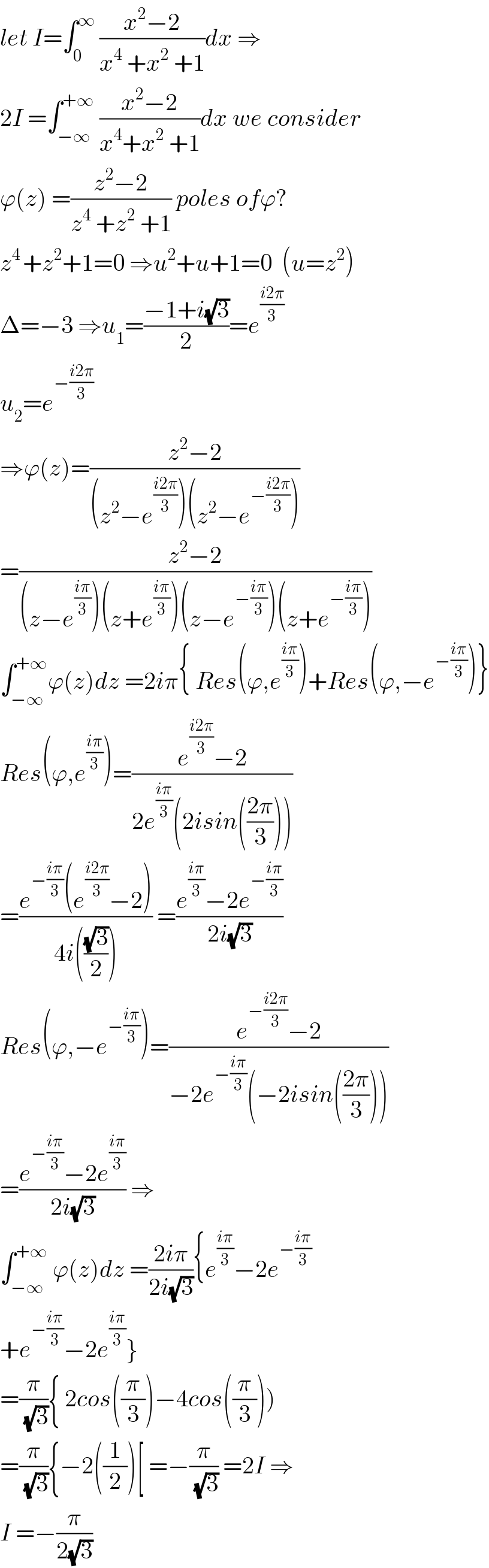
let I=∫_0 ^∞ ((x^2 −2)/(x^4 +x^2 +1))dx ⇒ 2I =∫_(−∞) ^(+∞) ((x^2 −2)/(x^4 +x^2 +1))dx we consider ϕ(z) =((z^2 −2)/(z^4 +z^2 +1)) poles ofϕ? z^(4 ) +z^2 +1=0 ⇒u^2 +u+1=0 (u=z^2 ) Δ=−3 ⇒u_1 =((−1+i(√3))/2)=e^((i2π)/3) u_2 =e^(−((i2π)/3)) ⇒ϕ(z)=((z^2 −2)/((z^2 −e^((i2π)/3) )(z^2 −e^(−((i2π)/3)) ))) =((z^2 −2)/((z−e^((iπ)/3) )(z+e^((iπ)/3) )(z−e^(−((iπ)/3)) )(z+e^(−((iπ)/3)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/3) )+Res(ϕ,−e^(−((iπ)/3)) )} Res(ϕ,e^((iπ)/3) )=((e^((i2π)/3) −2)/(2e^((iπ)/3) (2isin(((2π)/3))))) =((e^(−((iπ)/3)) (e^((i2π)/3) −2))/(4i(((√3)/2)))) =((e^((iπ)/3) −2e^(−((iπ)/3)) )/(2i(√3))) Res(ϕ,−e^(−((iπ)/3)) )=((e^(−((i2π)/3)) −2)/(−2e^(−((iπ)/3)) (−2isin(((2π)/3))))) =((e^(−((iπ)/3)) −2e^((iπ)/3) )/(2i(√3))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =((2iπ)/(2i(√3))){e^((iπ)/3) −2e^(−((iπ)/3)) +e^(−((iπ)/3)) −2e^((iπ)/3) } =(π/( (√3))){ 2cos((π/3))−4cos((π/3))) =(π/( (√3))){−2((1/2))[ =−(π/( (√3))) =2I ⇒ I =−(π/(2(√3)))
$${let}\:{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:{we}\:{consider} \\ $$$$\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} −\mathrm{2}}{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:{poles}\:{of}\varphi? \\ $$$${z}^{\mathrm{4}\:} +{z}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\Rightarrow{u}^{\mathrm{2}} +{u}+\mathrm{1}=\mathrm{0}\:\:\left({u}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=−\mathrm{3}\:\Rightarrow{u}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${u}_{\mathrm{2}} ={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\Rightarrow\varphi\left({z}\right)=\frac{{z}^{\mathrm{2}} −\mathrm{2}}{\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{z}^{\mathrm{2}} −\mathrm{2}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)=\frac{{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} −\mathrm{2}}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} \left(\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)} \\ $$$$=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} \left({e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} −\mathrm{2}\right)}{\mathrm{4}{i}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} −\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)=\frac{{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} −\mathrm{2}}{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \left(−\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)} \\ $$$$=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} −\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\mathrm{2}{i}\pi}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{{e}^{\frac{{i}\pi}{\mathrm{3}}} −\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right. \\ $$$$\left.+{e}^{−\frac{{i}\pi}{\mathrm{3}}} −\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} \right\} \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{3}}}\left\{\:\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)−\mathrm{4}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\right) \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{3}}}\left\{−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\:=−\frac{\pi}{\:\sqrt{\mathrm{3}}}\:=\mathrm{2}{I}\:\Rightarrow\right.\right. \\ $$$${I}\:=−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *