0-x-2-e-x-2-1-dx-

Question Number 95949 by Ar Brandon last updated on 28/May/20

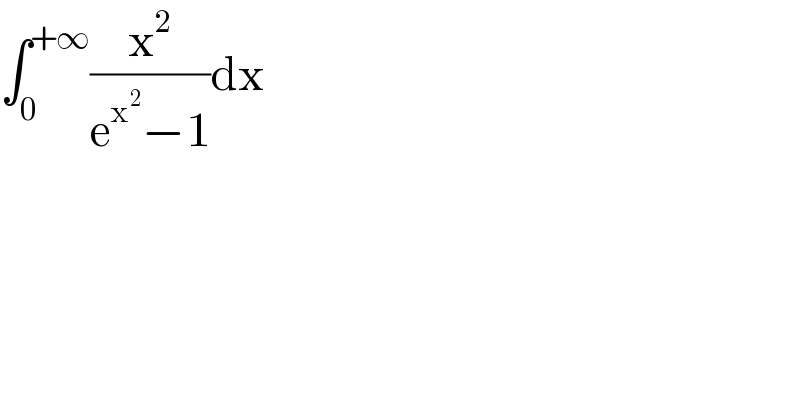
$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } −\mathrm{1}}\mathrm{dx} \\ $$

Answered by Sourav mridha last updated on 28/May/20

let, x^2 =t so dx=(1/(2(√t))) dt when x=0 then t=0 and x⇒+∞ then t⇒+∞ now are integral looks like−− (1/2)∫_0 ^(+∞) (t^(1/2) /(e^t −1)) dt =((Γ((3/2)))/2)[(1/(Γ((3/2))))∫_0 ^(+∞) (t^((3/2)−1) /(e^t −1))dt] =((√π)/4)𝛇((3/2))

$$\:\:\mathrm{let},\:\mathrm{x}^{\mathrm{2}} =\mathrm{t}\:\mathrm{so}\:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{t}}}\:\mathrm{dt} \\ $$$$\mathrm{when}\:\mathrm{x}=\mathrm{0}\:\mathrm{then}\:\mathrm{t}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{x}\Rightarrow+\infty\:\mathrm{then}\:\mathrm{t}\Rightarrow+\infty\: \\ $$$$\mathrm{now}\:\mathrm{are}\:\mathrm{integral}\:\:\mathrm{looks}\:\mathrm{like}−− \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{e}^{\mathrm{t}} \:−\mathrm{1}}\:\mathrm{dt} \\ $$$$=\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}}\left[\frac{\mathrm{1}}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{e}^{\mathrm{t}} \:−\mathrm{1}}\mathrm{dt}\right] \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{4}}\boldsymbol{\zeta}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$

Commented by Ar Brandon last updated on 29/May/20

Thanks mridha

Answered by abdomathmax last updated on 28/May/20

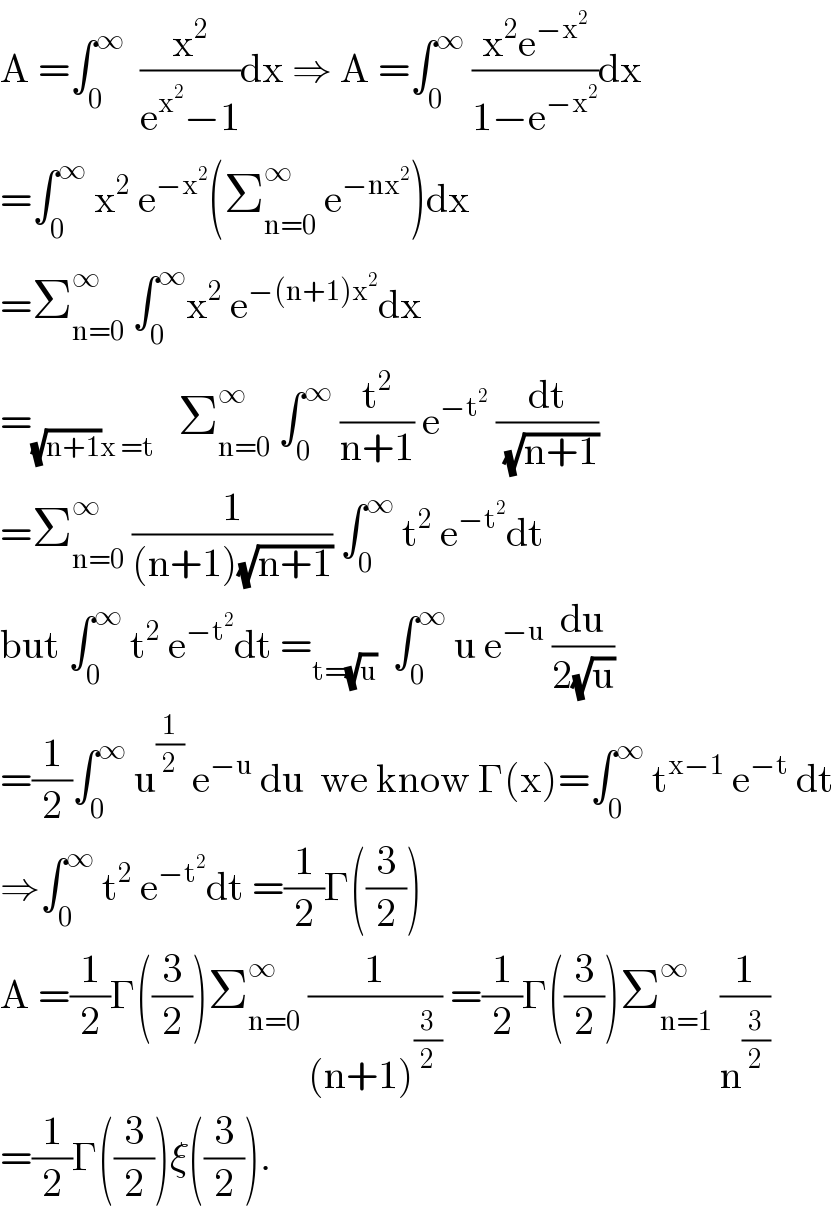
A =∫_0 ^∞ (x^2 /(e^x^2 −1))dx ⇒ A =∫_0 ^∞ ((x^2 e^(−x^2 ) )/(1−e^(−x^2 ) ))dx =∫_0 ^∞ x^2 e^(−x^2 ) (Σ_(n=0) ^∞ e^(−nx^2 ) )dx =Σ_(n=0) ^∞ ∫_0 ^∞ x^2 e^(−(n+1)x^2 ) dx =_((√(n+1))x =t) Σ_(n=0) ^∞ ∫_0 ^∞ (t^2 /(n+1)) e^(−t^2 ) (dt/( (√(n+1)))) =Σ_(n=0) ^∞ (1/((n+1)(√(n+1)))) ∫_0 ^∞ t^2 e^(−t^2 ) dt but ∫_0 ^∞ t^2 e^(−t^2 ) dt =_(t=(√u)) ∫_0 ^∞ u e^(−u) (du/(2(√u))) =(1/2)∫_0 ^∞ u^(1/2) e^(−u) du we know Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt ⇒∫_0 ^∞ t^2 e^(−t^2 ) dt =(1/2)Γ((3/2)) A =(1/2)Γ((3/2))Σ_(n=0) ^∞ (1/((n+1)^(3/2) )) =(1/2)Γ((3/2))Σ_(n=1) ^∞ (1/n^(3/2) ) =(1/2)Γ((3/2))ξ((3/2)).

$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } −\mathrm{1}}\mathrm{dx}\:\Rightarrow\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }{\mathrm{1}−\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{nx}^{\mathrm{2}} } \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$=_{\sqrt{\mathrm{n}+\mathrm{1}}\mathrm{x}\:=\mathrm{t}} \:\:\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{n}+\mathrm{1}}\:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{n}+\mathrm{1}}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{n}+\mathrm{1}}}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt} \\ $$$$\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=_{\mathrm{t}=\sqrt{\mathrm{u}}} \:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}\:\mathrm{e}^{−\mathrm{u}} \:\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{u}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du}\:\:\mathrm{we}\:\mathrm{know}\:\Gamma\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\: \\ $$$$\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\xi\left(\frac{\mathrm{3}}{\mathrm{2}}\right). \\ $$

Commented by Ar Brandon last updated on 29/May/20

Thank you mathmax

Commented by mathmax by abdo last updated on 29/May/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply