Question Number 189752 by TUN last updated on 21/Mar/23
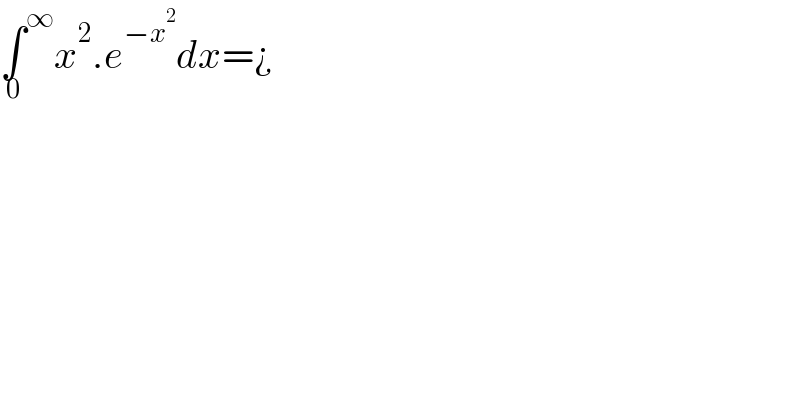
$$\underset{\mathrm{0}} {\int}^{\infty} {x}^{\mathrm{2}} .{e}^{−{x}^{\mathrm{2}} } {dx}=¿ \\ $$
Answered by MJS_new last updated on 21/Mar/23
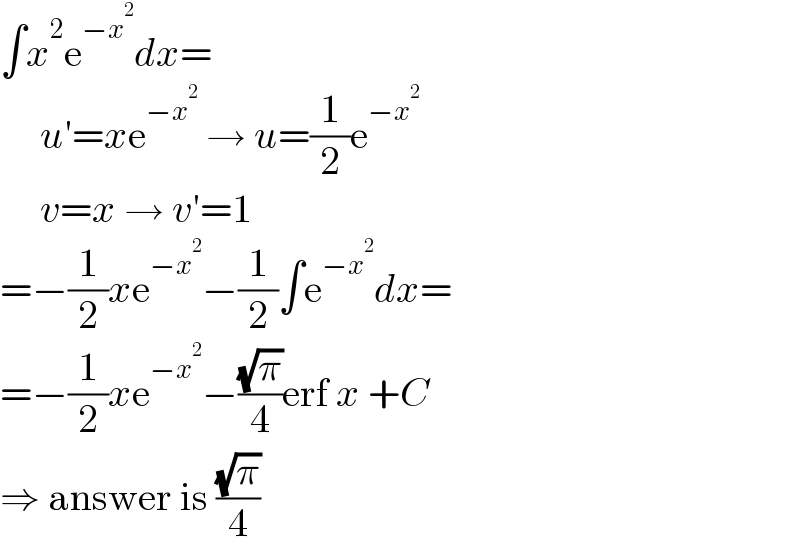
$$\int{x}^{\mathrm{2}} \mathrm{e}^{−{x}^{\mathrm{2}} } {dx}= \\ $$$$\:\:\:\:\:{u}'={x}\mathrm{e}^{−{x}^{\mathrm{2}} } \:\rightarrow\:{u}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:{v}={x}\:\rightarrow\:{v}'=\mathrm{1} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{x}\mathrm{e}^{−{x}^{\mathrm{2}} } −\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{e}^{−{x}^{\mathrm{2}} } {dx}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{x}\mathrm{e}^{−{x}^{\mathrm{2}} } −\frac{\sqrt{\pi}}{\mathrm{4}}\mathrm{erf}\:{x}\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\sqrt{\pi}}{\mathrm{4}} \\ $$
