Question Number 130598 by Lordose last updated on 27/Jan/21
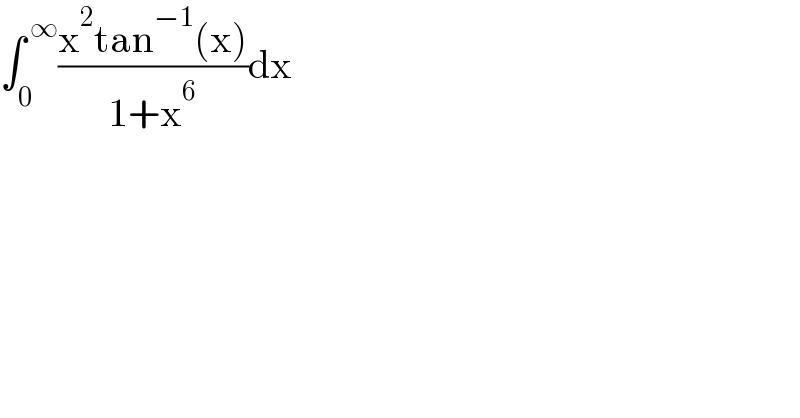
$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\mathrm{dx} \\ $$
Answered by mindispower last updated on 27/Jan/21
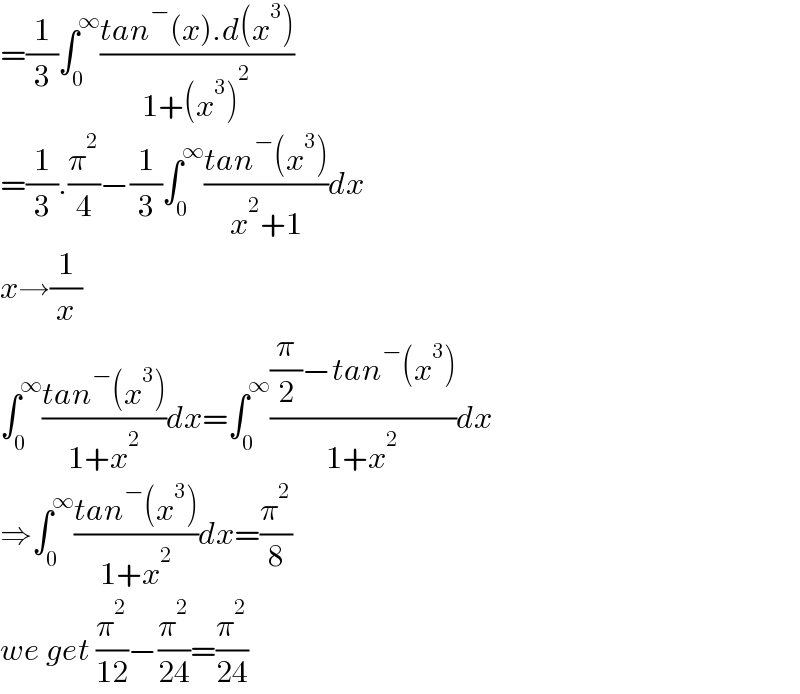
$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−} \left({x}\right).{d}\left({x}^{\mathrm{3}} \right)}{\mathrm{1}+\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−} \left({x}^{\mathrm{3}} \right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${x}\rightarrow\frac{\mathrm{1}}{{x}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−} \left({x}^{\mathrm{3}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\frac{\pi}{\mathrm{2}}−{tan}^{−} \left({x}^{\mathrm{3}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−} \left({x}^{\mathrm{3}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${we}\:{get}\:\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\pi^{\mathrm{2}} }{\mathrm{24}}=\frac{\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$
Commented by mnjuly1970 last updated on 27/Jan/21
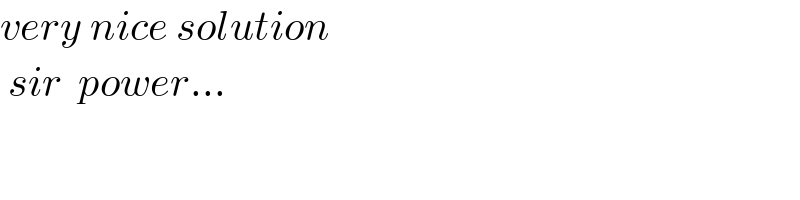
$${very}\:{nice}\:{solution} \\ $$$$\:{sir}\:\:{power}… \\ $$
Answered by mathmax by abdo last updated on 27/Jan/21
![I =∫_0 ^∞ ((x^2 arctan(x))/(1+x^6 ))dx ⇒I =(1/3)∫_0 ^∞ ((x^2 arctan(x))/(1+(x^3 )^2 ))(dx^3 ) =(1/3){[ arctan(x^3 )arctanx]_0 ^∞ −∫_0 ^∞ ((arctan(x^3 ))/(1+x^2 ))dx} ⇒3I =(π^2 /4)−∫_0 ^∞ ((arctan(x^3 ))/(1+x^2 ))dx Φ=∫_0 ^∞ ((arctan(x^3 ))/(1+x^2 ))dx =_(x=(1/t)) −∫_0 ^∞ (((π/2)−arctant^3 )/(1+(1/t^2 )))(−(dt/t^2 )) =∫_0 ^∞ (((π/2)−arctan(t^3 ))/(1+t^2 ))dt =(π/2)∫_0 ^∞ (dt/(1+t^2 ))−Φ ⇒ 2Φ =(π/2)×(π/2) =(π^2 /4) ⇒Φ=(π^2 /8) ⇒3I=(π^2 /4)−(π^2 /8)=(π^2 /8) ⇒I =(π^2 /(24))](https://www.tinkutara.com/question/Q130620.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{arctan}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{arctan}\left(\mathrm{x}\right)}{\mathrm{1}+\left(\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{2}} }\left(\mathrm{dx}^{\mathrm{3}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left\{\left[\:\mathrm{arctan}\left(\mathrm{x}^{\mathrm{3}} \right)\mathrm{arctanx}\right]_{\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\right\} \\ $$$$\Rightarrow\mathrm{3I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}} \:\:−\int_{\mathrm{0}} ^{\infty} \:\frac{\frac{\pi}{\mathrm{2}}−\mathrm{arctant}^{\mathrm{3}} }{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{t}^{\mathrm{3}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\Phi\:\Rightarrow \\ $$$$\mathrm{2}\Phi\:=\frac{\pi}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\Phi=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow\mathrm{3I}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow\mathrm{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$
