Menu Close

0-x-2-x-4-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 65203 by arcana last updated on 26/Jul/19
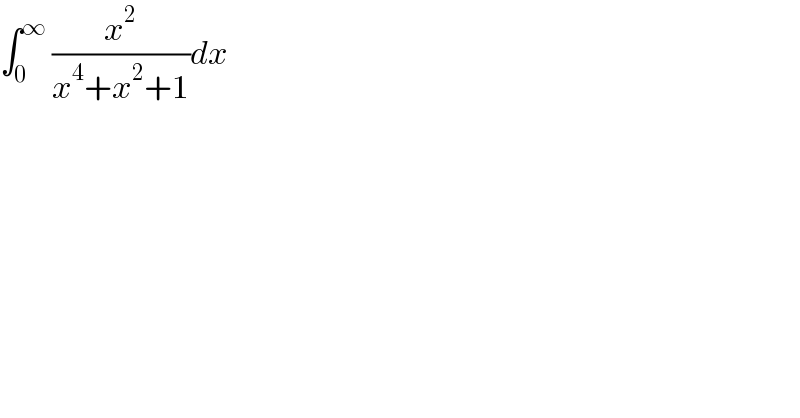
∫_0 ^∞ (x^2 /(x^4 +x^2 +1))dx
$$\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$
Commented by mathmax by abdo last updated on 26/Jul/19
let I =∫_0 ^∞ (x^2 /(x^4 +x^2 +1))dx ⇒2I =∫_(−∞) ^(+∞) (x^2 /(x^4 +x^2 +1))dx let ϕ(z) =(z^2 /(z^4 +z^2 +1)) poles of ϕ? z^4 +z^2 +1 =0 ⇒t^2 +t +1 =0 (t=z^2 ) Δ =1−4 =−3 =(i(√3))^2 ⇒t_1 =((−1+i(√3))/2) and t_2 =((−1−i(√3))/2) t_1 =e^((i2π)/3) and t_2 =e^(−((2iπ)/3)) ⇒t^2 +t+1 =(t−e^((i2π)/3) )(t−e^(−((i2π)/3)) ) =(z^2 −e^((i2π)/3) )(z^2 −e^(−((i2π)/3)) ) ⇒ϕ(z) =(z^2 /((z−e^((iπ)/3) )(z+e^((iπ)/3) )(z−e^(−((iπ)/3)) )(z+e^(−((iπ)/3)) ))) the poles of ϕ are +^− e^((iπ)/3) and +^− e^(−((iπ)/3)) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/3) ) +Res(ϕ,−e^(−((iπ)/3)) )} Res(ϕ,e^((iπ)/3) ) =lim_(z→e^((iπ)/3) ) (z−e^((iπ)/3) )ϕ(z)=(e^((2iπ)/3) /(2e^((iπ)/3) (e^((2iπ)/3) −e^(−((2iπ)/3)) ))) =(e^((iπ)/3) /(2(2isin(((2π)/3))))) =(e^((iπ)/3) /(4i((√3)/2))) =(e^((iπ)/3) /(2i(√3))) Res(ϕ,−e^(−((iπ)/3)) ) =lim_(z→e^(−((iπ)/3)) ) (z+e^(−((iπ)/3)) ) = (e^(−((2iπ)/3)) /((e^(−((2iπ)/3)) −e^((i2π)/3) )(−2e^(−((iπ)/3)) ))) =(e^(−((iπ)/3)) /(−2i((√3)/2)(−2))) =(e^(−((iπ)/3)) /(2i(√3))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{(e^((iπ)/3) /(2i(√3))) +(e^(−((iπ)/3)) /(2i(√3)))} =(π/( (√3))){2cos((π/3)) =(π/( (√3))) (2.(1/2)) =(π/( (√3))) ⇒ I =(1/2) ∫_(−∞) ^(+∞) ϕ(z)dz =(π/(2(√3))) .
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:\Rightarrow\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:{let} \\ $$$$\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:\:\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} +{t}\:+\mathrm{1}\:=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4}\:=−\mathrm{3}\:=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${t}_{\mathrm{1}} ={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\:\:{and}\:\:{t}_{\mathrm{2}} ={e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \:\:\Rightarrow{t}^{\mathrm{2}} \:+{t}+\mathrm{1}\:=\left({t}−{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left({t}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right) \\ $$$$=\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\:\Rightarrow\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{3}}} \:{and}\:\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right\} \\ $$$$\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\varphi\left({z}\right)=\frac{{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} }{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} \left({e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} −{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}\left(\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{4}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:={lim}_{{z}\rightarrow{e}^{−\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:=\:\frac{{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} }{\left({e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} −{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{−\mathrm{2}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(−\mathrm{2}\right)}\:=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:+\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\right\} \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{3}}}\left\{\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\:=\frac{\pi}{\:\sqrt{\mathrm{3}}}\:\left(\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\frac{\pi}{\:\sqrt{\mathrm{3}}}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:.\right. \\ $$
Answered by Tanmay chaudhury last updated on 26/Jul/19
∫_0 ^∞ (dx/(x^2 +1+(1/x^2 ))) (1/2)∫_0 ^∞ ((1+(1/x^2 )+1−(1/x^2 ))/(x^2 +(1/x^2 )+1))dx (1/2)∫_0 ^∞ ((d(x−(1/x)))/((x−(1/x))^2 +3))+(1/2)∫_0 ^∞ ((d(x+(1/x)))/((x+(1/x))^2 −1)) (1/2)×(1/( (√3)))∣tan^(−1) (((x−(1/x))/( (√3))))+(1/2)×(1/(2×1))ln(((x+(1/x)−1)/(x+(1/x)+1)))∣_0 ^∞ =(1/(2(√3)))tan^(−1) (∞)−(1/(2(√3)))tan^(−1) (−∞)+(1/4)ln(((1+(1/x^2 )−(1/x))/(1+(1/x^2 )+(1/x))))_(x=∞) −(1/4)ln(((x^2 +1−x)/(x^2 +1+x)))_(x=0) =(1/(2(√3)))×(π/2)+(1/(2(√3)))×(π/2))+(1/4)×ln1−(1/4)ln1 =(π/(2(√3)))
$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}×\mathrm{1}}{ln}\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\infty\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(−\infty\right)+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}}\right)_{{x}=\infty} −\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}−{x}}{{x}^{\mathrm{2}} +\mathrm{1}+{x}}\right)_{{x}=\mathrm{0}} \\ $$$$\left.=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{4}}×{ln}\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mathrm{1} \\ $$$$=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$
Commented by arcana last updated on 26/Jul/19
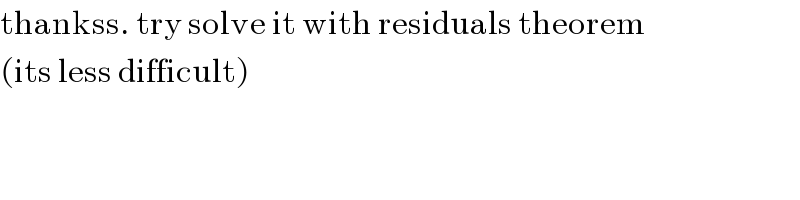
thankss. try solve it with residuals theorem (its less difficult)
$$\mathrm{thankss}.\:\mathrm{try}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{with}\:\mathrm{residuals}\:\mathrm{theorem} \\ $$$$\left(\mathrm{its}\:\mathrm{less}\:\mathrm{difficult}\right) \\ $$
Commented by Tanmay chaudhury last updated on 26/Jul/19
ok sir...
$${ok}\:{sir}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *