Question Number 103220 by Dwaipayan Shikari last updated on 13/Jul/20

$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} }{{e}^{{x}} +\mathrm{1}}{dx} \\ $$
Answered by mathmax by abdo last updated on 13/Jul/20
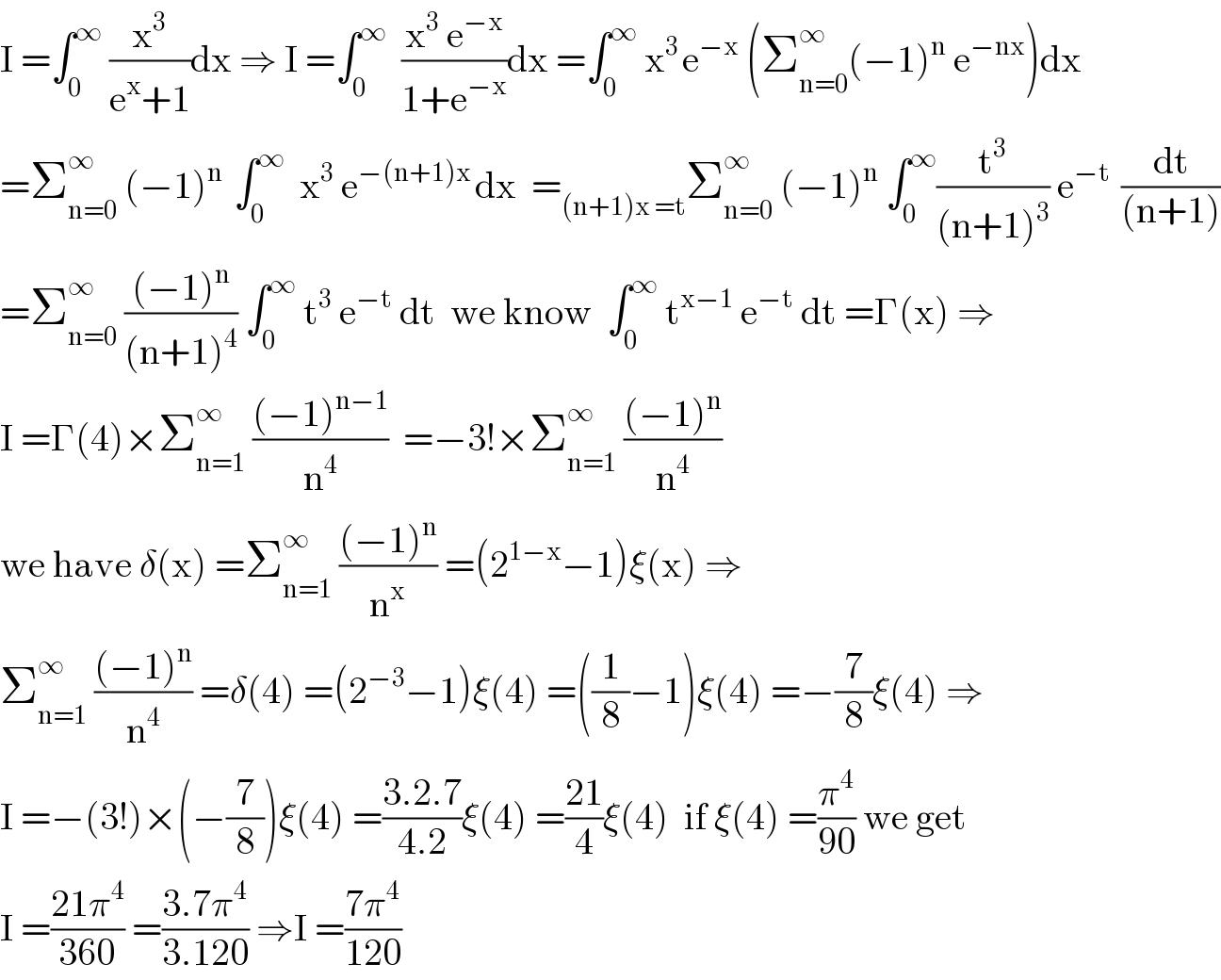
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}\mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{3}} \:\mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{3}\:} \mathrm{e}^{−\mathrm{x}} \:\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{nx}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}\:} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{x}^{\mathrm{3}} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}\:} \mathrm{dx}\:\:=_{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}\:=\mathrm{t}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{3}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{e}^{−\mathrm{t}\:} \:\frac{\mathrm{dt}}{\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} }\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{3}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{know}\:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:=\Gamma\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\Gamma\left(\mathrm{4}\right)×\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{4}} }\:\:=−\mathrm{3}!×\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{4}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\delta\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{x}} }\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{x}} −\mathrm{1}\right)\xi\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{4}} }\:=\delta\left(\mathrm{4}\right)\:=\left(\mathrm{2}^{−\mathrm{3}} −\mathrm{1}\right)\xi\left(\mathrm{4}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{8}}−\mathrm{1}\right)\xi\left(\mathrm{4}\right)\:=−\frac{\mathrm{7}}{\mathrm{8}}\xi\left(\mathrm{4}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=−\left(\mathrm{3}!\right)×\left(−\frac{\mathrm{7}}{\mathrm{8}}\right)\xi\left(\mathrm{4}\right)\:=\frac{\mathrm{3}.\mathrm{2}.\mathrm{7}}{\mathrm{4}.\mathrm{2}}\xi\left(\mathrm{4}\right)\:=\frac{\mathrm{21}}{\mathrm{4}}\xi\left(\mathrm{4}\right)\:\:\mathrm{if}\:\xi\left(\mathrm{4}\right)\:=\frac{\pi^{\mathrm{4}} }{\mathrm{90}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{I}\:=\frac{\mathrm{21}\pi^{\mathrm{4}} }{\mathrm{360}}\:=\frac{\mathrm{3}.\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{3}.\mathrm{120}}\:\Rightarrow\mathrm{I}\:=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{120}} \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jul/20

$${Thanking}\:{you} \\ $$
Commented by abdomsup last updated on 13/Jul/20

$${you}\:{are}\:{welcome} \\ $$
