Menu Close

0-x-3-sin-x-x-4-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 127468 by bramlexs22 last updated on 30/Dec/20
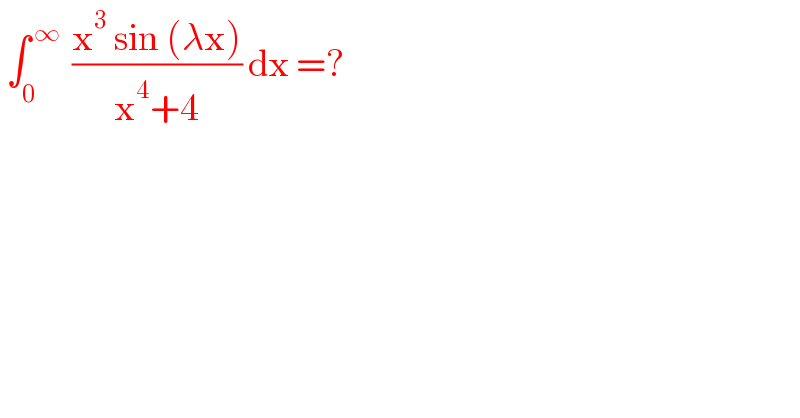
∫_0 ^( ∞) ((x^3 sin (λx))/(x^4 +4)) dx =?
$$\:\int_{\mathrm{0}} ^{\:\infty} \:\:\frac{\mathrm{x}^{\mathrm{3}} \:\mathrm{sin}\:\left(\lambda\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{4}}\:\mathrm{dx}\:=?\: \\ $$
Commented by bramlexs22 last updated on 30/Dec/20
thank you both sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both}\:\mathrm{sir} \\ $$
Answered by Olaf last updated on 30/Dec/20
Let g(λ,x) = ((x^3 sin(λx))/(x^4 +4)) Let f(λ) = ∫_0 ^∞ g(λ,x)dx (1) f′(λ) = ∫_0 ^∞ (∂g/∂λ)(λ,x)dx = λ∫_0 ^∞ ((x^3 cos(λx))/(x^4 +4))dx f′′(λ) = ∫((x^3 cos(λx))/(x^4 +4))dx−λ^2 ∫_0 ^∞ ((x^3 sin(λx))/(x^4 +4))dx f′′(λ) = ((f′(λ))/λ)−λ^2 f(λ) λf′′(λ) −f′(λ)+λ^3 f(λ) = 0 (2) Let t = λ^2 , λ = t^(1/2) f′(λ) = (df/dλ) = (dt/dλ).(df/dt) = 2t^(1/2) (df/dt) (3) f′′(λ) = ((df′)/dλ) = (dt/dλ).((df′)/dt) = 2t^(1/2) [t^(−1/2) (df/dt)+2t^(1/2) (d^2 f/dt^2 )] f′′(λ) = 2[(df/dt)+2t(d^2 f/dt^2 )] (4) With (2), (3) and (4) : 2 t^(1/2) [(df/dt)+2t(d^2 f/dt^2 )]−2t^(1/2) (df/dt)+t^(3/2) f = 0 (d^2 f/dt^2 )+(1/4)f = 0 → f(t) = Acos((t/2))+Bsin((t/2)) f(λ) = Acos((λ^2 /2))+Bsin((λ^2 /2)) A ? B ? (1) : f(0) = ∫_0 ^∞ ((x^3 sin(0))/(x^4 +4))dx = 0 ⇒ A = 0 f(λ) = Bsin((λ^2 /2)) (1) : f(λ) = −f(λ) → f is odd ⇒ B = 0 ?????!!! Sorry ! I tried !
$$\mathrm{Let}\:{g}\left(\lambda,{x}\right)\:=\:\frac{{x}^{\mathrm{3}} \mathrm{sin}\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}} \\ $$$$\mathrm{Let}\:{f}\left(\lambda\right)\:=\:\int_{\mathrm{0}} ^{\infty} {g}\left(\lambda,{x}\right){dx}\:\left(\mathrm{1}\right) \\ $$$${f}'\left(\lambda\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\partial{g}}{\partial\lambda}\left(\lambda,{x}\right){dx}\:=\:\lambda\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} \mathrm{cos}\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}{dx} \\ $$$${f}''\left(\lambda\right)\:=\:\int\frac{{x}^{\mathrm{3}} \mathrm{cos}\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}{dx}−\lambda^{\mathrm{2}} \int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} \mathrm{sin}\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}{dx} \\ $$$${f}''\left(\lambda\right)\:=\:\frac{{f}'\left(\lambda\right)}{\lambda}−\lambda^{\mathrm{2}} {f}\left(\lambda\right) \\ $$$$\lambda{f}''\left(\lambda\right)\:−{f}'\left(\lambda\right)+\lambda^{\mathrm{3}} {f}\left(\lambda\right)\:=\:\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{Let}\:{t}\:=\:\lambda^{\mathrm{2}} ,\:\lambda\:=\:{t}^{\mathrm{1}/\mathrm{2}} \\ $$$${f}'\left(\lambda\right)\:=\:\frac{{df}}{{d}\lambda}\:=\:\frac{{dt}}{{d}\lambda}.\frac{{df}}{{dt}}\:=\:\mathrm{2}{t}^{\mathrm{1}/\mathrm{2}} \frac{{df}}{{dt}}\:\left(\mathrm{3}\right) \\ $$$${f}''\left(\lambda\right)\:=\:\frac{{df}'}{{d}\lambda}\:=\:\frac{{dt}}{{d}\lambda}.\frac{{df}'}{{dt}}\:=\:\mathrm{2}{t}^{\mathrm{1}/\mathrm{2}} \left[{t}^{−\mathrm{1}/\mathrm{2}} \frac{{df}}{{dt}}+\mathrm{2}{t}^{\mathrm{1}/\mathrm{2}} \frac{{d}^{\mathrm{2}} {f}}{{dt}^{\mathrm{2}} }\right] \\ $$$${f}''\left(\lambda\right)\:=\:\mathrm{2}\left[\frac{{df}}{{dt}}+\mathrm{2}{t}\frac{{d}^{\mathrm{2}} {f}}{{dt}^{\mathrm{2}} }\right]\:\left(\mathrm{4}\right) \\ $$$$\mathrm{With}\:\left(\mathrm{2}\right),\:\left(\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{4}\right)\:\:: \\ $$$$\mathrm{2}\:{t}^{\mathrm{1}/\mathrm{2}} \left[\frac{{df}}{{dt}}+\mathrm{2}{t}\frac{{d}^{\mathrm{2}} {f}}{{dt}^{\mathrm{2}} }\right]−\mathrm{2}{t}^{\mathrm{1}/\mathrm{2}} \frac{{df}}{{dt}}+{t}^{\mathrm{3}/\mathrm{2}} {f}\:=\:\mathrm{0} \\ $$$$\frac{{d}^{\mathrm{2}} {f}}{{dt}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}{f}\:=\:\mathrm{0} \\ $$$$\rightarrow\:{f}\left({t}\right)\:=\:\mathrm{Acos}\left(\frac{{t}}{\mathrm{2}}\right)+\mathrm{Bsin}\left(\frac{{t}}{\mathrm{2}}\right) \\ $$$${f}\left(\lambda\right)\:=\:\mathrm{Acos}\left(\frac{\lambda^{\mathrm{2}} }{\mathrm{2}}\right)+\mathrm{Bsin}\left(\frac{\lambda^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\mathrm{A}\:?\:\mathrm{B}\:? \\ $$$$\left(\mathrm{1}\right)\::\:{f}\left(\mathrm{0}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} \mathrm{sin}\left(\mathrm{0}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}{dx}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{A}\:=\:\mathrm{0} \\ $$$${f}\left(\lambda\right)\:=\:\mathrm{Bsin}\left(\frac{\lambda^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\left(\mathrm{1}\right)\::\:{f}\left(\lambda\right)\:=\:−{f}\left(\lambda\right)\:\rightarrow\:{f}\:\mathrm{is}\:\mathrm{odd} \\ $$$$\Rightarrow\:\mathrm{B}\:=\:\mathrm{0}\:?????!!! \\ $$$$\mathrm{Sorry}\:!\:\mathrm{I}\:\mathrm{tried}\:! \\ $$
Answered by bramlexs22 last updated on 30/Dec/20
super nice integral
$$\:\mathrm{super}\:\mathrm{nice}\:\mathrm{integral} \\ $$
Answered by liberty last updated on 30/Dec/20
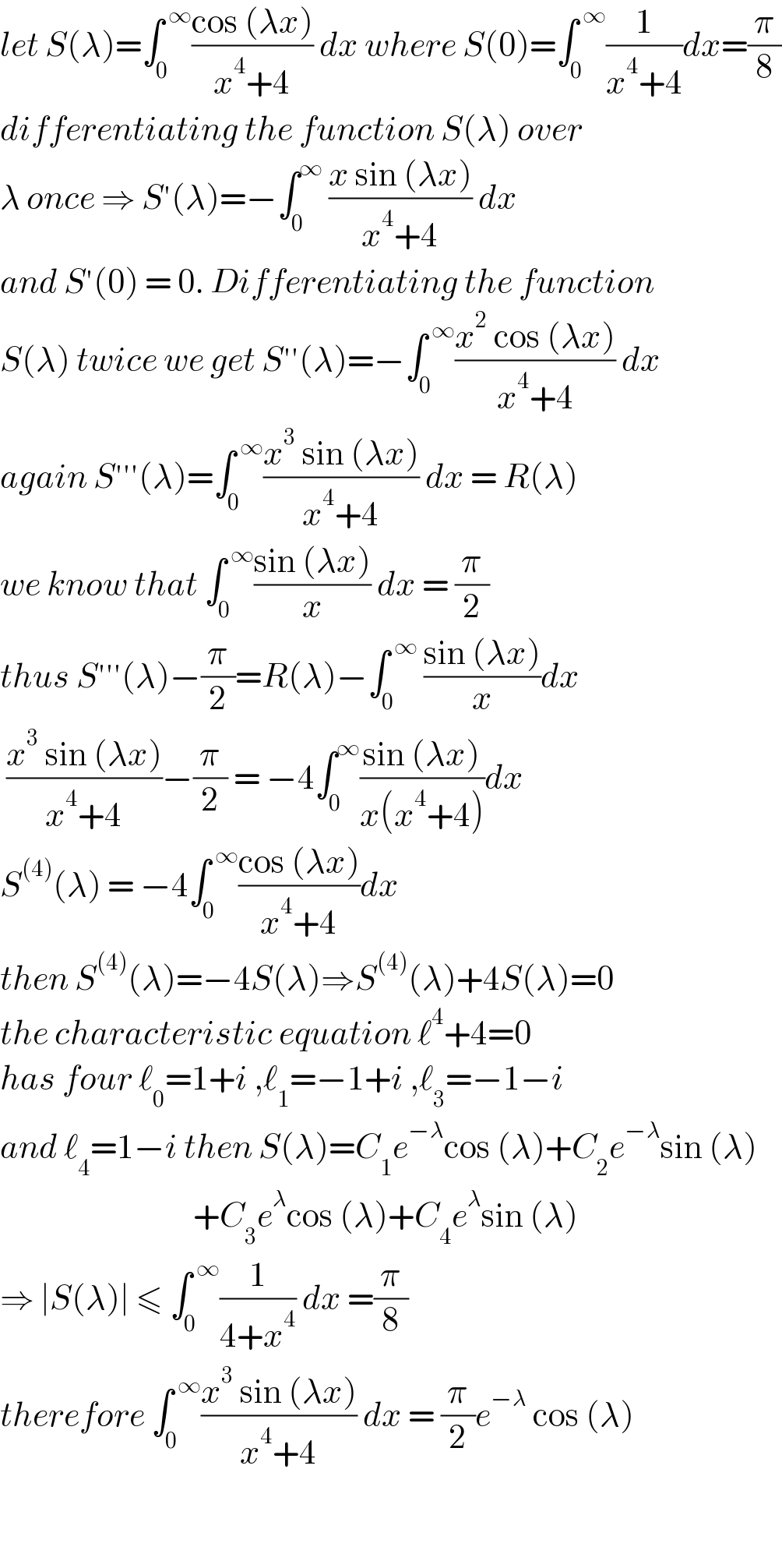
let S(λ)=∫_0 ^( ∞) ((cos (λx))/(x^4 +4)) dx where S(0)=∫_0 ^( ∞) (1/(x^4 +4))dx=(π/8) differentiating the function S(λ) over λ once ⇒ S′(λ)=−∫_0 ^∞ ((x sin (λx))/(x^4 +4)) dx and S′(0) = 0. Differentiating the function S(λ) twice we get S′′(λ)=−∫_0 ^( ∞) ((x^2 cos (λx))/(x^4 +4)) dx again S′′′(λ)=∫_0 ^( ∞) ((x^3 sin (λx))/(x^4 +4)) dx = R(λ) we know that ∫_0 ^( ∞) ((sin (λx))/x) dx = (π/2) thus S′′′(λ)−(π/2)=R(λ)−∫_0 ^( ∞) ((sin (λx))/x)dx ((x^3 sin (λx))/(x^4 +4))−(π/2) = −4∫_0 ^∞ ((sin (λx))/(x(x^4 +4)))dx S^((4)) (λ) = −4∫_0 ^( ∞) ((cos (λx))/(x^4 +4))dx then S^((4)) (λ)=−4S(λ)⇒S^((4)) (λ)+4S(λ)=0 the characteristic equation ℓ^4 +4=0 has four ℓ_0 =1+i ,ℓ_1 =−1+i ,ℓ_3 =−1−i and ℓ_4 =1−i then S(λ)=C_1 e^(−λ) cos (λ)+C_2 e^(−λ) sin (λ) +C_3 e^λ cos (λ)+C_4 e^λ sin (λ) ⇒ ∣S(λ)∣ ≤ ∫_0 ^( ∞) (1/(4+x^4 )) dx =(π/8) therefore ∫_0 ^( ∞) ((x^3 sin (λx))/(x^4 +4)) dx = (π/2)e^(−λ) cos (λ)
$${let}\:{S}\left(\lambda\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{cos}\:\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}\:{dx}\:{where}\:{S}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{4}}{dx}=\frac{\pi}{\mathrm{8}} \\ $$$${differentiating}\:{the}\:{function}\:{S}\left(\lambda\right)\:{over} \\ $$$$\lambda\:{once}\:\Rightarrow\:{S}'\left(\lambda\right)=−\int_{\mathrm{0}} ^{\infty} \:\frac{{x}\:\mathrm{sin}\:\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}\:{dx} \\ $$$${and}\:{S}'\left(\mathrm{0}\right)\:=\:\mathrm{0}.\:{Differentiating}\:{the}\:{function} \\ $$$${S}\left(\lambda\right)\:{twice}\:{we}\:{get}\:{S}''\left(\lambda\right)=−\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}\:{dx} \\ $$$${again}\:{S}'''\left(\lambda\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{\mathrm{3}} \:\mathrm{sin}\:\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}\:{dx}\:=\:{R}\left(\lambda\right) \\ $$$${we}\:{know}\:{that}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{sin}\:\left(\lambda{x}\right)}{{x}}\:{dx}\:=\:\frac{\pi}{\mathrm{2}} \\ $$$${thus}\:{S}'''\left(\lambda\right)−\frac{\pi}{\mathrm{2}}={R}\left(\lambda\right)−\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{sin}\:\left(\lambda{x}\right)}{{x}}{dx} \\ $$$$\:\frac{{x}^{\mathrm{3}} \:\mathrm{sin}\:\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}−\frac{\pi}{\mathrm{2}}\:=\:−\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:\left(\lambda{x}\right)}{{x}\left({x}^{\mathrm{4}} +\mathrm{4}\right)}{dx} \\ $$$${S}^{\left(\mathrm{4}\right)} \left(\lambda\right)\:=\:−\mathrm{4}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{cos}\:\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}{dx}\: \\ $$$${then}\:{S}^{\left(\mathrm{4}\right)} \left(\lambda\right)=−\mathrm{4}{S}\left(\lambda\right)\Rightarrow{S}^{\left(\mathrm{4}\right)} \left(\lambda\right)+\mathrm{4}{S}\left(\lambda\right)=\mathrm{0} \\ $$$${the}\:{characteristic}\:{equation}\:\ell^{\mathrm{4}} +\mathrm{4}=\mathrm{0} \\ $$$${has}\:{four}\:\ell_{\mathrm{0}} =\mathrm{1}+{i}\:,\ell_{\mathrm{1}} =−\mathrm{1}+{i}\:,\ell_{\mathrm{3}} =−\mathrm{1}−{i} \\ $$$${and}\:\ell_{\mathrm{4}} =\mathrm{1}−{i}\:{then}\:{S}\left(\lambda\right)={C}_{\mathrm{1}} {e}^{−\lambda} \mathrm{cos}\:\left(\lambda\right)+{C}_{\mathrm{2}} {e}^{−\lambda} \mathrm{sin}\:\left(\lambda\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{C}_{\mathrm{3}} {e}^{\lambda} \mathrm{cos}\:\left(\lambda\right)+{C}_{\mathrm{4}} {e}^{\lambda} \mathrm{sin}\:\left(\lambda\right) \\ $$$$\Rightarrow\:\mid{S}\left(\lambda\right)\mid\:\leqslant\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\mathrm{4}+{x}^{\mathrm{4}} }\:{dx}\:=\frac{\pi}{\mathrm{8}} \\ $$$${therefore}\:\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{\mathrm{3}} \:\mathrm{sin}\:\left(\lambda{x}\right)}{{x}^{\mathrm{4}} +\mathrm{4}}\:{dx}\:=\:\frac{\pi}{\mathrm{2}}{e}^{−\lambda} \:\mathrm{cos}\:\left(\lambda\right)\: \\ $$$$ \\ $$$$ \\ $$
Commented by Olaf last updated on 30/Dec/20
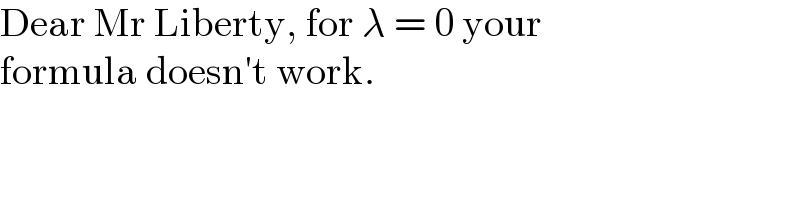
Dear Mr Liberty, for λ = 0 your formula doesn′t work.
$$\mathrm{Dear}\:\mathrm{Mr}\:\mathrm{Liberty},\:\mathrm{for}\:\lambda\:=\:\mathrm{0}\:\mathrm{your}\: \\ $$$$\mathrm{formula}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work}. \\ $$
Commented by liberty last updated on 30/Dec/20
yes sir. i think this question valid for λ > 0 .
$${yes}\:{sir}.\:{i}\:{think}\:{this}\:{question}\:{valid}\:{for} \\ $$$$\lambda\:>\:\mathrm{0}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *