Menu Close

0-x-5-ln-x-cos-x-e-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 130485 by benjo_mathlover last updated on 26/Jan/21
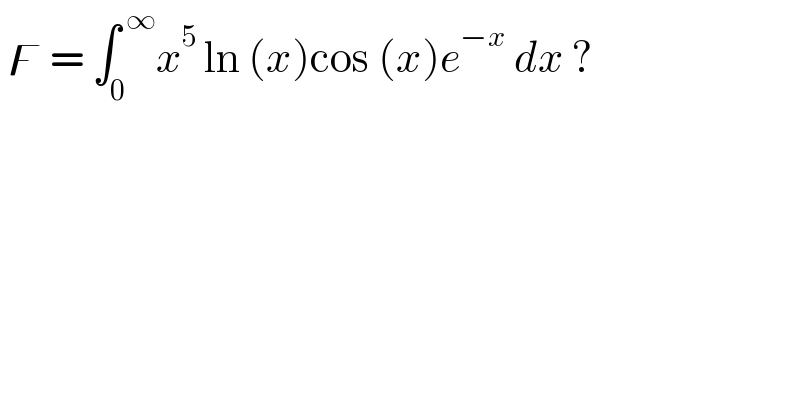
ϝ = ∫_0 ^( ∞) x^(5 ) ln (x)cos (x)e^(−x) dx ?
$$\:\digamma\:=\:\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{5}\:} \mathrm{ln}\:\left({x}\right)\mathrm{cos}\:\left({x}\right){e}^{−{x}} \:{dx}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 26/Jan/21
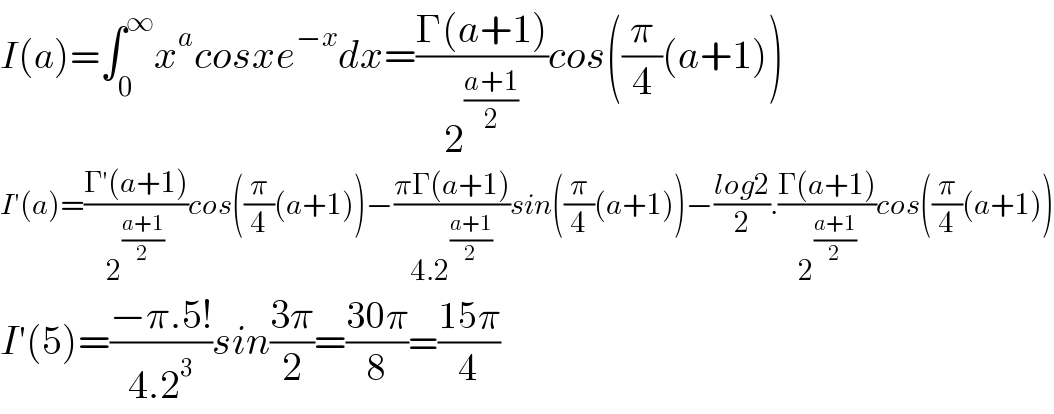
I(a)=∫_0 ^∞ x^a cosxe^(−x) dx=((Γ(a+1))/2^((a+1)/2) )cos((π/4)(a+1)) I′(a)=((Γ′(a+1))/2^((a+1)/2) )cos((π/4)(a+1))−((πΓ(a+1))/(4.2^((a+1)/2) ))sin((π/4)(a+1))−((log2)/2).((Γ(a+1))/2^((a+1)/2) )cos((π/4)(a+1)) I′(5)=((−π.5!)/(4.2^3 ))sin((3π)/2)=((30π)/8)=((15π)/4)
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {x}^{{a}} {cosxe}^{−{x}} {dx}=\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{cos}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right) \\ $$$${I}'\left({a}\right)=\frac{\Gamma'\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{cos}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right)−\frac{\pi\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{4}.\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{sin}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right)−\frac{{log}\mathrm{2}}{\mathrm{2}}.\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{cos}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right) \\ $$$${I}'\left(\mathrm{5}\right)=\frac{−\pi.\mathrm{5}!}{\mathrm{4}.\mathrm{2}^{\mathrm{3}} }{sin}\frac{\mathrm{3}\pi}{\mathrm{2}}=\frac{\mathrm{30}\pi}{\mathrm{8}}=\frac{\mathrm{15}\pi}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 26/Jan/21
F=∫_0 ^∞ x^5 ln(x)cosx e^(−x) dx let F(a)=∫_0 ^∞ x^a cosx e^(−x) dx ⇒ F(a)=Re(∫_0 ^∞ x^a e^(ix−x) dx) and ∫_0 ^∞ x^a e^((−1+i)x) dx =_((1−i)x=t) ∫_0 ^∞ ((t/(1−i)))^a e^(−t) (dt/(1−i)) =(1/((1−i)^(a+1) ))∫_0 ^∞ t^a e^(−t) dt =Γ(a+1)×(1/(((√2)e^(−((iπ)/4)) )^(a+1) )) =((Γ(a+1))/2^((a+1)/2) ) e^(i(((a+1)/4))π) ⇒F(a)=((Γ(a+1))/2^((a+1)/2) )cos((π/4)(a+1)) (a>−1) F(a)=∫_0 ^∞ e^(alnx) cosx e^(−x) dx ⇒F^′ (a)=∫_0 ^∞ lnx .x^a cosx e^(−x) dx ⇒ ⇒F =F^′ (5) we have F(a)=2^(−((a+1)/2)) Γ(a+1)cos((π/4)a+(π/4)) ⇒ F^′ (a)=(2^(−((a+1)/2)) Γ(a+1))^′ cos(((πa)/4)+(π/4))−(π/4)2^(−((a+1)/2)) Γ(a+1)sin(((πa)/4)+(π/4)) 2^(−((a+1)/2)) Γ(a+1)=e^(−((a+1)/2)ln(2)) Γ(a+1) ⇒ (d/da)(...)=−((ln2)/2).2^(−((a+1)/2)) .Γ(a+1)+e^(−((a+1)/2)) Γ^′ (a+1)=.... be continued...
$$\mathrm{F}=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{5}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{cosx}\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}\:\:\mathrm{let}\:\mathrm{F}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{a}} \mathrm{cosx}\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{a}\right)=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{a}} \mathrm{e}^{\mathrm{ix}−\mathrm{x}} \mathrm{dx}\right)\:\mathrm{and}\:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{a}} \:\mathrm{e}^{\left(−\mathrm{1}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=_{\left(\mathrm{1}−\mathrm{i}\right)\mathrm{x}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{t}}{\mathrm{1}−\mathrm{i}}\right)^{\mathrm{a}} \mathrm{e}^{−\mathrm{t}} \:\:\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{i}}\:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{a}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{a}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt} \\ $$$$=\Gamma\left(\mathrm{a}+\mathrm{1}\right)×\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{a}+\mathrm{1}} }\:=\frac{\Gamma\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} }\:\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{4}}\right)\pi} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{a}\right)=\frac{\Gamma\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} }\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\left(\mathrm{a}+\mathrm{1}\right)\right)\:\:\:\left(\mathrm{a}>−\mathrm{1}\right) \\ $$$$\mathrm{F}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{alnx}} \:\mathrm{cosx}\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}\:\Rightarrow\mathrm{F}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{lnx}\:.\mathrm{x}^{\mathrm{a}} \:\mathrm{cosx}\:\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}\:\Rightarrow \\ $$$$\Rightarrow\mathrm{F}\:=\mathrm{F}^{'} \left(\mathrm{5}\right)\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{F}\left(\mathrm{a}\right)=\mathrm{2}^{−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} \:\Gamma\left(\mathrm{a}+\mathrm{1}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\mathrm{a}+\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$$\mathrm{F}^{'} \left(\mathrm{a}\right)=\left(\mathrm{2}^{−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} \Gamma\left(\mathrm{a}+\mathrm{1}\right)\right)^{'} \:\mathrm{cos}\left(\frac{\pi\mathrm{a}}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}\right)−\frac{\pi}{\mathrm{4}}\mathrm{2}^{−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} \Gamma\left(\mathrm{a}+\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{2}^{−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} \Gamma\left(\mathrm{a}+\mathrm{1}\right)=\mathrm{e}^{−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)} \:\Gamma\left(\mathrm{a}+\mathrm{1}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{d}}{\mathrm{da}}\left(…\right)=−\frac{\mathrm{ln2}}{\mathrm{2}}.\mathrm{2}^{−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} .\Gamma\left(\mathrm{a}+\mathrm{1}\right)+\mathrm{e}^{−\frac{\mathrm{a}+\mathrm{1}}{\mathrm{2}}} \Gamma^{'} \left(\mathrm{a}+\mathrm{1}\right)=…. \\ $$$$\mathrm{be}\:\mathrm{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *