Menu Close

0-x-a-1-x-3-dx-x-0-lt-a-lt-3-

Tinku Tara 0 Comments
Pin




Question Number 147061 by liberty last updated on 17/Jul/21
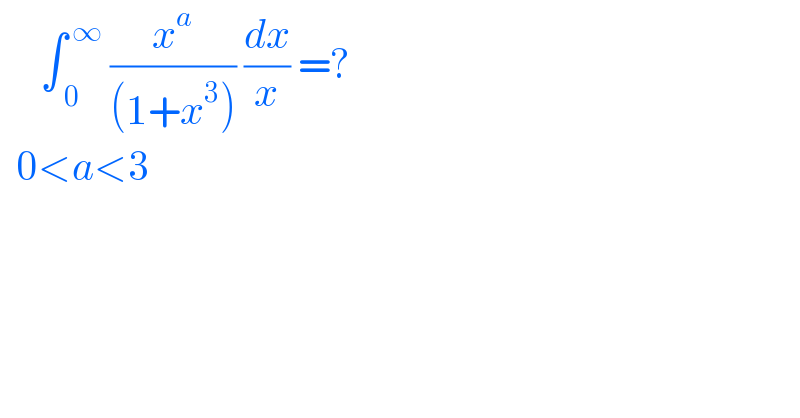
∫_( 0 ) ^( ∞) (x^a /((1+x^3 ))) (dx/x) =? 0<a<3
$$\:\:\:\:\:\int_{\:\mathrm{0}\:} ^{\:\infty} \:\frac{{x}^{{a}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\:\frac{{dx}}{{x}}\:=?\: \\ $$$$\:\:\mathrm{0}<{a}<\mathrm{3}\:\: \\ $$
Answered by Ar Brandon last updated on 17/Jul/21
I=∫_0 ^∞ (x^a /((1+x^3 )))∙(dx/x), x=u^(1/3) ⇒dx=(1/3)u^(−(2/3)) du =(1/3)∫_0 ^∞ (u^((a/3)−1) /((1+u)))du=(1/3)β((a/3), 1−(a/3)) =(1/3)∙((Γ((a/3))Γ(1−(a/3)))/(Γ(1)))=(1/3)∙(π/(sin((a/3)π)))
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{a}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)}\centerdot\frac{\mathrm{dx}}{\mathrm{x}},\:\mathrm{x}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{3}}} \Rightarrow\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{u}^{−\frac{\mathrm{2}}{\mathrm{3}}} \mathrm{du} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\frac{\mathrm{a}}{\mathrm{3}}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{u}\right)}\mathrm{du}=\frac{\mathrm{1}}{\mathrm{3}}\beta\left(\frac{\mathrm{a}}{\mathrm{3}},\:\mathrm{1}−\frac{\mathrm{a}}{\mathrm{3}}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\Gamma\left(\frac{\mathrm{a}}{\mathrm{3}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{a}}{\mathrm{3}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\pi}{\mathrm{sin}\left(\frac{\mathrm{a}}{\mathrm{3}}\pi\right)} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/21
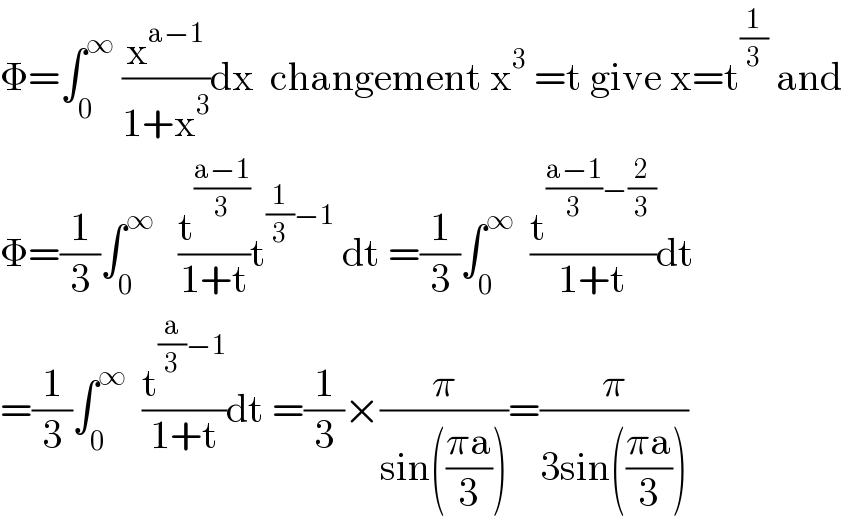
Φ=∫_0 ^∞ (x^(a−1) /(1+x^3 ))dx changement x^3 =t give x=t^(1/3) and Φ=(1/3)∫_0 ^∞ (t^((a−1)/3) /(1+t))t^((1/3)−1) dt =(1/3)∫_0 ^∞ (t^(((a−1)/3)−(2/3)) /(1+t))dt =(1/3)∫_0 ^∞ (t^((a/3)−1) /(1+t))dt =(1/3)×(π/(sin(((πa)/3))))=(π/(3sin(((πa)/3))))
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}^{\mathrm{3}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{and} \\ $$$$\Phi=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{t}^{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{3}}} }{\mathrm{1}+\mathrm{t}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\frac{\mathrm{a}}{\mathrm{3}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{3}}\right)}=\frac{\pi}{\mathrm{3sin}\left(\frac{\pi\mathrm{a}}{\mathrm{3}}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *